题目内容
8.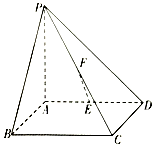 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.(1)求证:EF∥平面PAB;
(2)若PA=AB=2,求三棱锥P-AEF的体积.
分析 (1)取PB的中点为G,连接AG,FG,推导出EF∥AG,由此能证明EF∥平面PAB.
(2)由VP-AEF=VF-PAE,能求出三棱锥P-AEF的体积.
解答 证明:(1)取PB的中点为G,连接AG,FG,
∵E,F分别为AD,PC的中点,四棱锥P-ABCD的底面是正方形,
∴GF$\underset{∥}{=}$AE,∴AEFG是平行四边形,∴EF∥AG,
∵EF?平面PAB,AG?平面PAB,
∴EF∥平面PAB.
解:(2)∵PA=AB=2,PA⊥底面ABCD,
∴三棱锥P-AEF的体积${V_{P-AEF}}={V_{F-PAE}}=\frac{1}{3}×\frac{1}{2}×2×1×1=\frac{1}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
13.已知x,y为正实数,则$\frac{4x}{x+3y}+\frac{3y}{x}$的最小值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
17.将函数$f(x)=2sin({2x+\frac{π}{6}})$的图象向左平移$\frac{π}{12}$个单位,再向上平移1个单位,得到g(x)的图象.若g(x1)g(x2)=9,且x1,x2∈[-2π,2π],则2x1-x2的最大值为( )
| A. | $\frac{49π}{12}$ | B. | $\frac{35π}{6}$ | C. | $\frac{25π}{6}$ | D. | $\frac{17π}{4}$ |
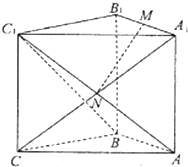 直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.
直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.