题目内容
15．已知函数f（x）=$\frac{lnx}{x}$，若方程f（x）=m存在两个不同的实数解，则实数m的取值范围为（ ）| A． | （0，$\frac{1}{e}$） | B． | （0，e） | C． | （-∞，$\frac{1}{e}$） | D． | （0，$\frac{1}{e}$] |
分析 对函数f（x）求导数f′（x），利用导数判断函数f（x）的单调性，求出f（x）的定义域和最大值，
即可求出方程f（x）=m存在两个不同的实数解时m的取值范围．
解答 解：∵函数f（x）=$\frac{lnx}{x}$，x＞0；
∴f′（x）=$\frac{\frac{1}{x}•x-lnx•1}{{x}^{2}}$=$\frac{1-lnx}{{x}^{2}}$，
令f′（x）=0，得1-lnx=0，
解得x=e；
当x∈（0，e）时，f′（x）＞0，f（x）是增函数；
当x∈（e，+∞）时，f′（x）＜0，f（x）是减函数；
当x=e时，f（x）取得最大值是f（e）=$\frac{1}{e}$，且f（x）＞0；
当方程f（x）=m存在两个不同的实数解时，
实数m的取值范围是0＜x＜$\frac{1}{e}$．
故选：A．
点评 本题考查了函数的零点的判断问题，也考查了利用导数判断函数的单调性与最值的应用问题，是综合性题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．将函数$f（x）=2sin（{2x+\frac{π}{6}}）$的图象向左平移$\frac{π}{12}$个单位，再向上平移1个单位，得到g（x）的图象．若g（x1）g（x2）=9，且x1，x2∈[-2π，2π]，则2x1-x2的最大值为（ ）
| A． | $\frac{49π}{12}$ | B． | $\frac{35π}{6}$ | C． | $\frac{25π}{6}$ | D． | $\frac{17π}{4}$ |
设函数f（x）=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$（a＞b＞0）的图象是曲线C．
10．设A，B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴两端点，Q为椭圆上一点，使∠AQB=120°，则椭圆离心率e的取值范围为（ ）
| A． | [$\frac{\sqrt{3}}{2}$，1） | B． | [$\frac{\sqrt{6}}{3}$，1） | C． | （0，$\frac{\sqrt{3}}{2}$] | D． | （0，$\frac{\sqrt{6}}{3}$] |
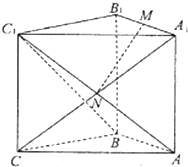直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=BB1，M为A1B1的中点，N是AC1与A1C的交点．
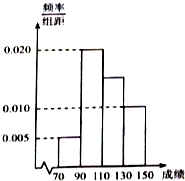某班一次数学考试成绩频率分布直方图如图所示，数据分组依次为[70，90），[90，110），[110，130），[130，150]，已知成绩大于等于90分的人数为36人，现采用分层抽样的方式抽取一个容量为10的样本．