题目内容
9.在△ABC中,|BC|是|AB|、|AC|的等差中项,且B(-1,0),C(1,0).(1)求顶点A的轨迹G的方程;
(2)若G上存在两点关于直线l:y=2x+m对称,求实数m的取值范围.
分析 (1)利用椭圆的定义,求顶点A的轨迹G的方程;
(2)由题意设关于直线y=2x+m对称的点为A,B,则AB的方程为y=-$\frac{1}{2}x$+n,联立椭圆方程与直线方程,由判别式大于0求得n的范围,利用根与系数的关系求出AB的中点C的坐标,再分别代入两条直线方程,得到n与m的关系,再由n的范围求得m的范围.
解答 解:(1)由题意,|AB|+|AC|=2|BC|=4>|BC|,
∴顶点A的轨迹G是以B,C为焦点的椭圆(除去A,B,C共线),且a=2,c=1,
∴b=$\sqrt{3}$,
∴顶点A的轨迹G的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1(x≠±2);
(2)解:设关于直线y=2x+m对称的点为A,B,则AB的方程为y=-$\frac{1}{2}x$+n,
与椭圆方程联立,消去y整理得:4x2-4nx+4n2-12=0.
即x2-nx+(n2-3)=0.
由△=n2-4n2+12>0,得-2<n<2.
设A(x1,y1),B(x2,y2),
则x1+x2=n,x1x2=n2-3,
再设AB的中点为C(x0,y0),
则x0=$\frac{n}{2}$,
又C在y=-$\frac{1}{2}x$+n上,得y0=$\frac{3}{4}$n,
C在y=2x+m上,得$\frac{3}{4}$n=2×$\frac{n}{2}$+m,即n=-4m.
则-2<-2m<2,得-$\frac{1}{2}$<m<$\frac{1}{2}$.
点评 本题考查椭圆方程,考查直线与椭圆位置关系的应用,考查了存在性问题的求解方法,训练了点关于线的对称点的求法,是中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
17.将函数$f(x)=2sin({2x+\frac{π}{6}})$的图象向左平移$\frac{π}{12}$个单位,再向上平移1个单位,得到g(x)的图象.若g(x1)g(x2)=9,且x1,x2∈[-2π,2π],则2x1-x2的最大值为( )
| A. | $\frac{49π}{12}$ | B. | $\frac{35π}{6}$ | C. | $\frac{25π}{6}$ | D. | $\frac{17π}{4}$ |
10.设A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴两端点,Q为椭圆上一点,使∠AQB=120°,则椭圆离心率e的取值范围为( )
| A. | [$\frac{\sqrt{3}}{2}$,1) | B. | [$\frac{\sqrt{6}}{3}$,1) | C. | (0,$\frac{\sqrt{3}}{2}$] | D. | (0,$\frac{\sqrt{6}}{3}$] |
 已知函数f(x)=x2+2x|x-a|,其中a∈R.
已知函数f(x)=x2+2x|x-a|,其中a∈R. 设函数f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的图象是曲线C.
设函数f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的图象是曲线C.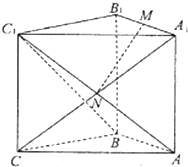 直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.
直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.