已知等差数列{an}的通项公式为an=51-3n.设Tn=|an+an+1+-+an+14|(n∈N*).则当Tn取得最小值时.n的值是( )A．10B．12C．15D．17 题目和参考答案——青夏教育精英家教网——

题目内容

16．已知等差数列{a_n}的通项公式为a_n=51-3n，设T_n=|a_n+a_n+1+…+a_n+14|（n∈N^*），则当T_n取得最小值时，n的值是（　　）

A．

10

B．

12

C．

15

D．

17

分析由等差数列的性质得T_n=|$\frac{15（{a}_{n}+{a}_{n+14}）}{2}$|=15|a_n+7|≥0，a₁₇=0，由此能求出结果．

解答解：∵等差数列{a_n}的通项公式为a_n=51-3n，T_n=|a_n+a_n+1+…+a_n+14|（n∈N^*），
∴T_n=|$\frac{15（{a}_{n}+{a}_{n+14}）}{2}$|=15|a_n+7|≥0，
∵a_n=51-3n，∴a₁₇=0，
∴当n+7=17，即n=10时，T_n取得最小值0．
故选：A．

点评本题考查等差数列的项数的求法，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案

英语奥林匹克系列答案

英才小状元系列答案

英才计划期末集中赢系列答案

银博士轻巧夺冠系列答案

一通百通考必赢系列答案

一线名师夺冠王检测卷系列答案

一线名师提优试卷系列答案

一路领先优选卷系列答案

一路领先口算题卡系列答案

一课3练课时导练系列答案

相关题目

17．将函数$f（x）=2sin（{2x+\frac{π}{6}}）$的图象向左平移$\frac{π}{12}$个单位，再向上平移1个单位，得到g（x）的图象．若g（x₁）g（x₂）=9，且x₁，x₂∈[-2π，2π]，则2x₁-x₂的最大值为（　　）

$\frac{49π}{12}$

$\frac{35π}{6}$

$\frac{25π}{6}$

$\frac{17π}{4}$

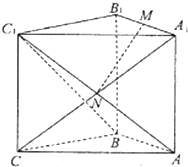直三棱柱ABC-A₁B₁C₁中，∠ABC=90°，AB=BC=BB₁，M为A₁B₁的中点，N是AC₁与A₁C的交点．
（Ⅰ）求证：MN∥平面BCC₁B₁；
（Ⅱ）求证：MN⊥平面ABC₁．

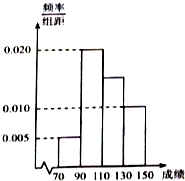某班一次数学考试成绩频率分布直方图如图所示，数据分组依次为[70，90），[90，110），[110，130），[130，150]，已知成绩大于等于90分的人数为36人，现采用分层抽样的方式抽取一个容量为10的样本．
（1）求每个分组所抽取的学生人数；
（2）从数学成绩在[110，150]的样本中任取2人，求恰有1人成绩在[110，130）的概率．

11．用秦九韶算法计算多项式f（x）=3x⁶+4x⁵+5x⁴+6x³+7x²+8x+1，当x=0.4时的值时，需要做乘法的次数是6次．

1．函数y=log₂（x-x²）的定义域为（　　）

8．已知f（x）=（a²-2a-2）^x是增函数，则实数a的取值范围是（-∞，-1）∪（3，+∞）．

5．化简：
（1）（$\frac{2}{3}$）^-2+（1-$\sqrt{2}$）⁰-（3$\frac{3}{8}$）${\;}^{\frac{2}{3}}$+$\sqrt{（3-π）^{2}}$；
（2）$\frac{5}{6}$a${\;}^{\frac{1}{3}}$b^-2•（-3a${\;}^{-\frac{1}{2}}$b^-1）÷（4a${\;}^{\frac{2}{3}}$b^-3）${\;}^{\frac{1}{2}}$．

6．在△ABC中，b=asinB，则△ABC一定是（　　）

钝角三角形

锐角三角形

直角三角形

等腰三角形