题目内容
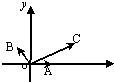如图所示，|| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OC |
| OC |
| OA |
| OB |
（1）求B点，C点坐标；
（2）求实数m、n的值．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）根据已知条件结合图形即可求出A，B，C三点的坐标；
（2）求出
，
，
的坐标，带入
=m
+n
，即可得到关于m，n的方程组，解方程组即得m，n的值．
（2）求出
| OA |
| OB |
| OC |
| OC |
| OA |
| OB |
解答：
解：（1）如图所示，由已知条件得：
A（1，0），B（-
，
），C(
，
)；
（2）(
，
)=m(1，0)+n(-
，
)；
∴
；
解得m=
，n=
．
A（1，0），B（-
| 1 |
| 2 |
| ||
| 2 |
5
| ||
| 2 |
| 5 |
| 2 |
（2）(
5
| ||
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
|
解得m=
10
| ||
| 3 |
5
| ||
| 3 |
点评：考查由点的坐标求向量的坐标，向量的坐标运算．
练习册系列答案
相关题目
下列函数中是奇函数是（ ）
A、y=x3-x+
| ||||||
B、y=
| ||||||
| C、y=x4-x2 | ||||||
| D、y=x6+x2+2 |
某同学通过计算机测试的概率为
，他连续测试3次，其中恰有1次通过的概率为（ ）
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=
，若直线y=m与函数y=f（x）三个不同交点的横坐标依次为x1，x2，x3，且x1＜x2＜x3，则x3的取值范围是（ ）
|
| A、（2，2014） |
| B、（1，2014） |
| C、（2，2013） |
| D、（1，2013） |
某种计算机病毒是通过电子邮件进行传播的，下表是某公司前5天监测到的数据：
若用下列四个函数中的一个来描述这些数据的规律，则其中最接近的一个是（ ）
| 第x天 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量y（台） | 10 | 20 | 39 | 81 | 160 |
| A、f（x）=10x |
| B、f（x）=5x2-5x+10 |
| C、f（x）=5•2x |
| D、f（x）=10log2x+10 |