题目内容
某同学通过计算机测试的概率为
,他连续测试3次,其中恰有1次通过的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:由条件根据相互独立事件的概率乘法公式,求得恰有1次通过的概率.
解答:
解:恰有1次通过的概率为
•
•(1-
)2=
,
故选:A.
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
故选:A.
点评:本题主要考查相互独立事件的概率乘法公式的应用,属于基础题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
下列说法正确的是( )
| A、若p∧q为假命题,则p、q都为假命题 | ||||||||
| B、“f(0)=0”是“函数f(x)为奇函数”充要条件 | ||||||||
| C、若命题p:?x0∈R,2x02+x0+3>0,则?p:?x∈R,2x2+x+3<0 | ||||||||
D、若“a=
|
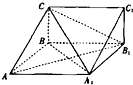 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3. 如图所示,
如图所示,