题目内容
下列函数中是奇函数是( )
A、y=x3-x+
| ||||||
B、y=
| ||||||
| C、y=x4-x2 | ||||||
| D、y=x6+x2+2 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:本题利用函数的奇偶性判断函数是否符合条件,不符合条件可以举出反倒,得到本题结论.
解答:
解:选项A,f(x)=x3-x+
,f(-x)=(-x)3-(-x)+
=-(x3-x+
)=-f(x),∴函数y=x3-x+
为奇函数;
选项B,y=
+
,定义域为(0,+∞)不关于0对称,故函数y=
+
不是奇函数;
选项C,f(x)=x4-x2,取x=2,f(x)=f(2)=24-22=16-4=12,f(-x)=f(-2)=(-2)4-(-2)2=16-4=12,f(-x)≠-f(x),函数y=x4-x2不是奇函数;
选项D,f(x)=x6+x2+2,取x=1,f(-1)=(-1)6+(-1)2+2=4,f(1)=16+12+2=4,f(-x)≠-f(x),函数y=)=x6+x2+2不是奇函数;
故选A.
| 1 |
| x |
| 1 |
| -x |
| 1 |
| x |
| 1 |
| x |
选项B,y=
| x |
| 1 | ||
|
| x |
| 1 | ||
|
选项C,f(x)=x4-x2,取x=2,f(x)=f(2)=24-22=16-4=12,f(-x)=f(-2)=(-2)4-(-2)2=16-4=12,f(-x)≠-f(x),函数y=x4-x2不是奇函数;
选项D,f(x)=x6+x2+2,取x=1,f(-1)=(-1)6+(-1)2+2=4,f(1)=16+12+2=4,f(-x)≠-f(x),函数y=)=x6+x2+2不是奇函数;
故选A.
点评:本题考查了函数的奇偶性,本题难度不大,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
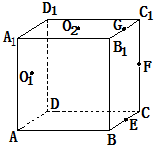 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点在同一个平面上的是
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点在同一个平面上的是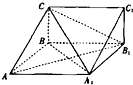 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.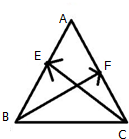 如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求
如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求 如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AB∥DC,PA⊥底面ABCD,且PA=AD=DC=
如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AB∥DC,PA⊥底面ABCD,且PA=AD=DC=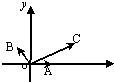 如图所示,
如图所示,