题目内容
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
若用下列四个函数中的一个来描述这些数据的规律,则其中最接近的一个是( )
| 第x天 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量y(台) | 10 | 20 | 39 | 81 | 160 |
| A、f(x)=10x |
| B、f(x)=5x2-5x+10 |
| C、f(x)=5•2x |
| D、f(x)=10log2x+10 |
考点:函数模型的选择与应用
专题:计算题,函数的性质及应用
分析:根据选项中的函数,依次代入x值求出y的值,通过y的值与表格中所给出的y的值进行比较,误差越小则拟合度越高,误差越大则拟合度越小,计算即可得到答案.
解答:
解:对于选项A,当x=1,2,3,4,5时,对应的y的值分别为10,20,30,40,50,
对于选项B,当x=1,2,3,4,5时,对应的y的值分别为10,20,40,70,110,
对于选项C,当x=1,2,3,4,5时,对应的y的值分别为10,20,40,80,185,
对于选项D,当x=1,2,3,4,5时,对应的y的值分别为10,20,10+10log23,30,10+10log25,
而表中所给的数据为,当x=1,2,3,4,5时,对应的y的值分别为10,20,39,81,160,
通过比较,即可发现选项C中y的值误差最小,即y=5•2x能更好的反映y与x之间的关系.
故选:C.
对于选项B,当x=1,2,3,4,5时,对应的y的值分别为10,20,40,70,110,
对于选项C,当x=1,2,3,4,5时,对应的y的值分别为10,20,40,80,185,
对于选项D,当x=1,2,3,4,5时,对应的y的值分别为10,20,10+10log23,30,10+10log25,
而表中所给的数据为,当x=1,2,3,4,5时,对应的y的值分别为10,20,39,81,160,
通过比较,即可发现选项C中y的值误差最小,即y=5•2x能更好的反映y与x之间的关系.
故选:C.
点评:本题考查了选择合适的模型来拟合一组数据,根据模型中的y的值和实际数据y的值进行比较,误差越小则拟合度越高,误差越大则拟合度越小.本题是一个比较简单的综合题目.

练习册系列答案
相关题目
下列说法正确的是( )
| A、若p∧q为假命题,则p、q都为假命题 | ||||||||
| B、“f(0)=0”是“函数f(x)为奇函数”充要条件 | ||||||||
| C、若命题p:?x0∈R,2x02+x0+3>0,则?p:?x∈R,2x2+x+3<0 | ||||||||
D、若“a=
|
已知a,b,c为△ABC中角A,B,C的对边,且cos2
=
,则△ABC为( )
| A |
| 2 |
| b+c |
| 2c |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
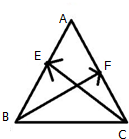 如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求
如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求 如图所示,
如图所示,