题目内容
定义在R上的奇函数f（x），当x≥0时，f（x）=x2，则不等式f（1-2x）＜f（3）的解集是 ．
考点：函数单调性的性质,函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由奇函数性质可知f（x）在（-∞，+∞）上单调递增，不等式f（1-2x）＜f（3）可得1-2x＜3，解得即可得到解集．
解答：
解：由于当x≥0时，f（x）=x2，则为增函数，
由奇函数性质可知f（x）在（-∞，+∞）上单调递增，
不等式f（1-2x）＜f（3可得1-2x＜3，解得x＞-1．
则解集为（-1，+∞），
故答案为：（-1，+∞）．
由奇函数性质可知f（x）在（-∞，+∞）上单调递增，
不等式f（1-2x）＜f（3可得1-2x＜3，解得x＞-1．
则解集为（-1，+∞），
故答案为：（-1，+∞）．
点评：本题考查函数的奇偶性和单调性的运用：解不等式，考查运算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列各选项中可以构成集合的是（ ）
| A、相当大的数 |
| B、本班视力较差的学生 |
| C、广州六中2014级学生 |
| D、著名的数学家 |
设函数f（x）=x2-2|x|-3．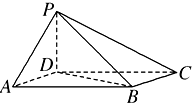
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2，AD=1，PD⊥底面ABCD．