题目内容
20.已知直线l经过抛物线y2=4x的焦点F,且与抛物线交于A,B两点(点A在第一象限)若$\overrightarrow{BA}=4\overrightarrow{BF}$,则△AOB的面积为( )| A. | $\frac{8}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{2}$ | D. | $\frac{4}{3}\sqrt{2}$ |
分析 求出抛物线的焦点,设直线l为x=my+1,代入抛物线方程,运用韦达定理和向量的坐标表示,解得m,再由三角形的面积公式,计算即可得到.
解答 解:抛物线y2=4x的焦点为(1,0),
设直线l为x=my+1,设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{x=my+1}\\{{y}^{2}=4x}\end{array}\right.$,整理得y2-4my-4=0,
则y1+y2=4m,y1y2=-4,
由$\overrightarrow{BA}=4\overrightarrow{BF}$,可得y1=-3y2,
由代入法,可得m2=$\frac{1}{3}$,
又△AOB的面积为S=$\frac{1}{2}$|OF|•|y1-y2|=$\frac{1}{2}$×1×$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{1}{2}$×$\sqrt{16{m}^{2}+16}$=$\frac{4\sqrt{3}}{3}$.
故选C.
点评 本题考查直线和抛物线的位置关系,主要考查韦达定理和向量的共线的坐标表示,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.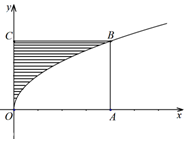 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
8.已知A(-1,0),B(3,2),C(0,-2),则过这三点的圆方程为( )
| A. | (x-$\frac{3}{2}$)2+y2=25 | B. | (x+$\frac{3}{2}$)2+y2=$\frac{1}{4}$ | C. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | D. | x2+(y-$\frac{3}{2}$)2=$\frac{5}{2}$ |
15.已知向量$\overrightarrow a=(2cosθ,2sinθ),\overrightarrow b=(0,-2)$,$θ∈(\frac{π}{2},π)$,则向量夹角为( )
| A. | $\frac{3π}{2}-θ$ | B. | $θ-\frac{π}{2}$ | C. | $\frac{π}{2}+θ$ | D. | θ |
5. 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )| A. | CE与BC1异面且垂直 | B. | AB1⊥C1F | ||
| C. | △C1DF是直角三角形 | D. | DF的长为$\frac{{\sqrt{6}}}{3}$ |
12.在区间[-1,3]上随机取一个数x,若x满足|x|<m的概率为0.75,则m=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
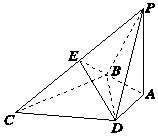 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.