题目内容
12．在区间[-1，3]上随机取一个数x，若x满足|x|＜m的概率为0.75，则m=（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 利用几何概型的概率公式得到关于m 的等式解之即可．根据区间[-1，3]的长度为4，可得当x满足|x|≤m的概率为时0.75，x所在的区间长度为3．解不等式|x|≤m得解集为[-m，m]，从而得到[-m，m]与[-1，3]的交集为[-1，2]，由此可解出m的值
解答 解：∵区间[-1，3]的区间长度为3-（-1）=4，
∴随机地取一个数x，若x满足|x|≤m的概率为0.75，
则满足条件的区间长度为4×0.75=3．
因此x所在的区间为[-1，2]，
∵m＞0，得|x|≤m的解集为{m|-m≤x≤m}=[-m，m]，
∴[-m，m]与[-1，3]的交集为[-1，2]时，可得m=2．
故选：C．
点评 本题给出几何概型的值，求参数m．着重考查了绝对值不等式的解法、集合的运算和几何概型计算公式等知识．
练习册系列答案
相关题目
3．若命题p：已知0＜a＜1，?x＜0，ax＞1，则￢p为（ ）
| A． | 已知a＞1，?x＞0，ax≤1 | B． | $已知0＜a＜1，?{x_0}＜0，{a^{x_0}}≤1$ | ||
| C． | $已知0＜a＜1，?{x_0}≥0，{a^{x_0}}≤1$ | D． | 已知a＞1，?x＞0，ax≤1 |
20．已知直线l经过抛物线y2=4x的焦点F，且与抛物线交于A，B两点（点A在第一象限）若$\overrightarrow{BA}=4\overrightarrow{BF}$，则△AOB的面积为（ ）
| A． | $\frac{8}{3}\sqrt{3}$ | B． | $\frac{4}{3}\sqrt{3}$ | C． | $\frac{8}{3}\sqrt{2}$ | D． | $\frac{4}{3}\sqrt{2}$ |
17．已知命题p：?x∈（-∞，0），2x＞3x；命题q：?x∈（0，$\frac{π}{2}$），sinx＞x，则下列命题为真命题的是（ ）
| A． | p∧q | B． | （￢p）∨q | C． | （￢p）∧q | D． | p∧（￢q） |
4．已知△ABC中，内角A，B，C所对的边分别为a，b，c，若$\frac{b}{c}$=$\frac{cosA}{1+cosC}$，则sin（2A+$\frac{π}{6}$）的取值范围是（ ）
| A． | （-$\frac{1}{2}$，$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，1] | C． | （$\frac{1}{2}$，1] | D． | [-1，$\frac{1}{2}$） |
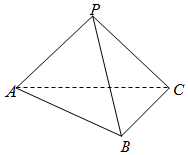如图，在三棱锥P-ABC中，平面ABC⊥平面APC，AB=BC=AP=PC=$\sqrt{2}$，∠ABC=∠APC=90°．