题目内容
数列{an}是各项均为正数的等比数列,公比q=3且a1a2a3…a30=330,则a3a6a9…a30=( )
| A、310 |
| B、315 |
| C、320 |
| D、325 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:由等比数列的通项公式把a1a2a3…a30=330用首项和公比表示,求出首项,把a3a6a9…a30用首项和公比表示,代入首项和公比得答案.
解答:
解:由a1a2a3…a30=330,q=3可知:
a1a2a3…a30=a130•q(1+2+…+29)
=a130•q435
=a130•3435=330,
∴a130=3-405.
∴a3a6a9…a30
=a110•q(2+5+…+29)
=a110•q155
=3-135×3155
=320.
故选:C.
a1a2a3…a30=a130•q(1+2+…+29)
=a130•q435
=a130•3435=330,
∴a130=3-405.
∴a3a6a9…a30
=a110•q(2+5+…+29)
=a110•q155
=3-135×3155
=320.
故选:C.
点评:本题考查了等比数列的通项公式,考查了等比数列的性质,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )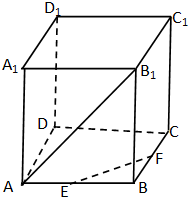

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a,b为非零实数,若a>b且ab>0,则下列不等式成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、ab2>a2b | ||||
D、
|
不等式组
,表示的平面区域的面积为( )
|
| A、4 | B、1 | C、5 | D、无穷大 |
函数f(x)=(
)x-x3-2的零点个数是( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |