题目内容
一个盒子中装有5个编号依次为1、2、3、4、5的球,这5个球除号码外完全相同,有放回的连续抽取两次,每次任意地取出一个球.
(1)用列表或画树状图的方法列出所有可能结果;
(2)设第一次取出的球号码为x,第二次取出的球号码为y,求事件A=“点(x,y)落在直线y=x+1上方”的概率.
(1)用列表或画树状图的方法列出所有可能结果;
(2)设第一次取出的球号码为x,第二次取出的球号码为y,求事件A=“点(x,y)落在直线y=x+1上方”的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)由题意知共有25种结果,用一对有序数对表示出可能出现的情况,第一个数字表示第一次抽到的数字,第二个数字表示第二次抽到的数字,写出所有的情况.
(2)本题是一个古典概型,由第一问可知试验发生包含的事件数是25,满足条件的事件是点(x,y)落在直线y=x+1上方的可以列举出所有结果,根据古典概型概率公式得到结果.
(2)本题是一个古典概型,由第一问可知试验发生包含的事件数是25,满足条件的事件是点(x,y)落在直线y=x+1上方的可以列举出所有结果,根据古典概型概率公式得到结果.
解答:
解:(1)由题意知共有25种结果,下面列举出所有情况:
(1,1)(1,2)(1,3)(1,4)(1,5)(2,1)(2,2)(2,3)(2,4)(2,5)
(3,1)(3,2)(3,3)(3,4)(3,5)(4,1)(4,2)(4,3)(4,4)(4,5)
(5,1)(5,2)(5,3)(5,4)(5,5)
(2)由题意知本题是一个古典概型,
试验发生包含的事件数是25,
满足条件的事件是点(x,y)落在直线y=x+1上方的有:
(1,3),(1,4),(1,5),(2,4),(2,5),(3,5)共6种.
∴P(B)=
.
(1,1)(1,2)(1,3)(1,4)(1,5)(2,1)(2,2)(2,3)(2,4)(2,5)
(3,1)(3,2)(3,3)(3,4)(3,5)(4,1)(4,2)(4,3)(4,4)(4,5)
(5,1)(5,2)(5,3)(5,4)(5,5)
(2)由题意知本题是一个古典概型,
试验发生包含的事件数是25,
满足条件的事件是点(x,y)落在直线y=x+1上方的有:
(1,3),(1,4),(1,5),(2,4),(2,5),(3,5)共6种.
∴P(B)=
| 6 |
| 25 |
点评:本题考查古典概型问题,这种问题在高考时可以作为一道解答题,古典概型要求能够列举出所有事件和发生事件的个数,本题可以列举出所有事件.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )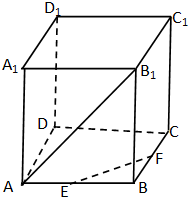

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点P(m,n)是直线2x+y+5=0上的任意一点,则
的最小值为( )
| (m-1)2+(n+2)2 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
不等式组
,表示的平面区域的面积为( )
|
| A、4 | B、1 | C、5 | D、无穷大 |
下列各组函数中,表示同一个函数的是( )
A、y=
| ||
B、y=lgx与y=
| ||
C、y=
| ||
| D、y=x与y=logaax(a>0且a≠1) |