题目内容
已知棱锥的顶点为P,P在底面上的射影为O,PO=a,现用平行于底面的平面去截这个棱锥,截面交PO于点M,并使截得的两部分侧面积相等,设OM=b,则a与b的关系是 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:利用用平行于底面的平面去截这个棱锥,截面交PO于点M,并使截得的两部分侧面积相等,可得截得棱锥的侧面积是原来侧面积的
,即相似比为
,即可确定a与b的关系.
| 1 |
| 2 |
| ||
| 2 |
解答:
解:∵用平行于底面的平面去截这个棱锥,截面交PO于点M,并使截得的两部分侧面积相等,
∴截得棱锥的侧面积是原来侧面积的
,
∴相似比为
,
∵PO=a,OM=b,
∴
=
,
∴b=(1-
)a.
故答案为:b=(1-
)a.
∴截得棱锥的侧面积是原来侧面积的
| 1 |
| 2 |
∴相似比为
| ||
| 2 |
∵PO=a,OM=b,
∴
| a-b |
| a |
| ||
| 2 |
∴b=(1-
| ||
| 2 |
故答案为:b=(1-
| ||
| 2 |
点评:本题考查棱锥的侧面积,考查图形的相似,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
侧棱和底面垂直的三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AC=1,BC=3,∠ACB=60°,C1C=2
,则球O的表面积为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
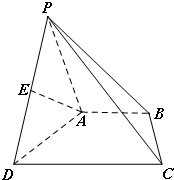 如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱
如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱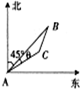 海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40
海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40