题目内容
已知向量
=(x2,x+1),
=(1-x,1),函数f(x)=
•
.
(1)求f(x)在x∈[0,2]的值域;
(2)若f(x)-t=0至少有两个实数解,求t的取值范围.
| a |
| b |
| a |
| b |
(1)求f(x)在x∈[0,2]的值域;
(2)若f(x)-t=0至少有两个实数解,求t的取值范围.
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)由已知条件,求出f(x)的表达式,再利用导数的性质能求出f(x)在x∈[0,2]的值域.
(2)f(x)-t=0至少有两个实数解,只需满足
,由此能求出t的取值范围.
(2)f(x)-t=0至少有两个实数解,只需满足
|
解答:
解:(1)∵向量
=(x2,x+1),
=(1-x,1),
∴f(x)=
•
=x2(1-x)+(x+1)=-x3+x2+x+1,
∴f′(x)=-3x2+2x+1,
由f′(x)=0,解得x1=-
,x2=1,
x∈(-
,1)时,f′(x)>0,f(x)是增函数,
x∈(-∞,-
),x∈(1,+∞)时,f′(x)<0,f(x)是减函数,
∵f(0)=1,f(1)=2,f(2)=-1,
∴f(x)在x∈[0,2]的值域为[-1,2].
(2)∵由f′(x)=0,解得x1=-
,x2=1,
∴f(x)-t=0至少有两个实数解,
只需满足
,
即
,
解得
≤t≤2,
∴t的取值范围是[
,2].
| a |
| b |
∴f(x)=
| a |
| b |
∴f′(x)=-3x2+2x+1,
由f′(x)=0,解得x1=-
| 1 |
| 3 |
x∈(-
| 1 |
| 3 |
x∈(-∞,-
| 1 |
| 3 |
∵f(0)=1,f(1)=2,f(2)=-1,
∴f(x)在x∈[0,2]的值域为[-1,2].
(2)∵由f′(x)=0,解得x1=-
| 1 |
| 3 |
∴f(x)-t=0至少有两个实数解,
只需满足
|
即
|
解得
| 22 |
| 27 |
∴t的取值范围是[
| 22 |
| 27 |
点评:本题借助平面向量数量积的坐标运算,考查函数的值域的求法,是中档题,解题时要注意导数性质的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
设函数f(x)的导函数为f′(x),且f(x)=x2+2x•f′(1),则f′(1)=( )
| A、0 | B、-4 | C、-2 | D、2 |
下列函数中,在区间(0,3)上为增函数的是( )
| A、y=-x+1 | ||
| B、y=x2+3 | ||
| C、y=x2-6x+10 | ||
D、y=
|
若sin(π+α)+sin(π-α)+sin(-α)=1,则sinα=( )
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
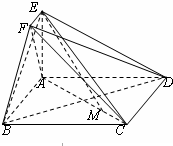 在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.
在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.