题目内容
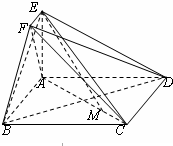 在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.
在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.(Ⅰ)若点M在线段AC上,且满足CM=
| 1 |
| 4 |
(Ⅱ)求证:AF⊥平面EBC;
(Ⅲ)求二面角A-FB-D的余弦值.
考点:直线与平面平行的判定,直线与平面垂直的判定,用空间向量求平面间的夹角
专题:空间角,空间向量及应用
分析:(I)过M作MN⊥BC,垂足为N,连结FN,则MN∥AB,又可得EF∥MN,从而四边形EFNM为平行四边形,所以EM∥FN,最后根据线面平行的判定定理,即可得到EM∥平面FBC;
(Ⅱ)先利用线面垂直的性质和勾股定理证出BC⊥AF,EB⊥AF,从而证出AF⊥平面EBC;
(Ⅲ)建立空间直角坐标系,求出两个平面的法向量,求解即可.
(Ⅱ)先利用线面垂直的性质和勾股定理证出BC⊥AF,EB⊥AF,从而证出AF⊥平面EBC;
(Ⅲ)建立空间直角坐标系,求出两个平面的法向量,求解即可.
解答:
 解:(Ⅰ)过M作MN⊥BC,垂足为N,连结FN,
解:(Ⅰ)过M作MN⊥BC,垂足为N,连结FN,
则MN∥AB.
又∵CM=
AC,
∴MN=
AB.
又∵EF∥AB且EF=
AB,
∴EF∥MN.且EF=MN.
∴四边形EFNM为平行四边形.
∴EM∥FN.
又FN?平面FBC,EM?平面FBC,
∴EM∥平面FBC.
(Ⅱ)∵EF∥AB,
∴EF与AB可确定平面EABF,
∵EA⊥平面ABCD,
∴EA⊥BC.
由已知得AB⊥BC且EA∩AB=A,
∴BC⊥平面EABF.
又AF?平面EABF,
∴BC⊥AF.
在四边形ABFE中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90°
设AF∩BE=P,
∵∠PAE+∠PAB=90°,
∴∠PBA+∠PAB=90°
则∠APB=90°,
∴EB⊥AF.
又∵EB∩BC=B,
∴AF⊥平面EBC.
(Ⅲ)以AB为x轴,AD为y轴,AE为z轴建立空间直角坐标系,
则B(4,0,0),D(0,4,0),F(1,0,2).
∴
=(-4,4,0),
=(1,-4,2)
设平面BDF的法向量为
(a,b,c),
则
,
解得:
=(2,2,-1).
同理可得,平面AFB的法向量为
=(0,1,0),
∴二面角A-FB-D=<
,
>,
∴二面角A-FB-D的余弦值为cos(π-<
,
>)=cos<
,
>=
=
=
.
 解:(Ⅰ)过M作MN⊥BC,垂足为N,连结FN,
解:(Ⅰ)过M作MN⊥BC,垂足为N,连结FN,则MN∥AB.
又∵CM=
| 1 |
| 4 |
∴MN=
| 1 |
| 4 |
又∵EF∥AB且EF=
| 1 |
| 4 |
∴EF∥MN.且EF=MN.
∴四边形EFNM为平行四边形.
∴EM∥FN.
又FN?平面FBC,EM?平面FBC,
∴EM∥平面FBC.
(Ⅱ)∵EF∥AB,
∴EF与AB可确定平面EABF,
∵EA⊥平面ABCD,
∴EA⊥BC.
由已知得AB⊥BC且EA∩AB=A,
∴BC⊥平面EABF.
又AF?平面EABF,
∴BC⊥AF.
在四边形ABFE中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90°
设AF∩BE=P,
∵∠PAE+∠PAB=90°,
∴∠PBA+∠PAB=90°
则∠APB=90°,
∴EB⊥AF.
又∵EB∩BC=B,
∴AF⊥平面EBC.
(Ⅲ)以AB为x轴,AD为y轴,AE为z轴建立空间直角坐标系,
则B(4,0,0),D(0,4,0),F(1,0,2).
∴
| BD |
| BF |
设平面BDF的法向量为
| m |
则
|
解得:
| m |
同理可得,平面AFB的法向量为
| n |
∴二面角A-FB-D=<
| m |
| n |
∴二面角A-FB-D的余弦值为cos(π-<
| m |
| n |
| m |
| n |
| ||||
|
|
| 2 |
| 3×1 |
| 2 |
| 3 |
点评:本题主要考查线面平行的判定定理及线面垂直的性质,考查二面角的求法,考查法向量的应用,是一个综合题目,题目的运算量不大,理解相关定理的内容是解决该类题目的基础.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
等比数列{an}的前n项和为Sn,若a1+a2+a3=3,a4+a5+a6=6,则S12=( )
| A、15 | B、30 | C、45 | D、60 |
某单位有老年人27人,中年人54人,青年人81人,为了调查他们身体状况的某项指标,需从他们中抽取一个容量为36的样本,适合抽取样本的方法是( )
| A、抽签法 | B、系统抽样 |
| C、随机数表法 | D、分层抽样 |
 已知椭圆C的中心在原点,焦点在x轴上,离心率
已知椭圆C的中心在原点,焦点在x轴上,离心率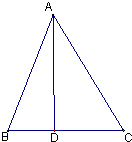 在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC
在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC