题目内容
已知正项等比数列{an}中 a2•a6=4,则log2a1+log2a2+…+log2a7=( )
| A、5 | B、6 | C、7 | D、8 |
考点:等差数列的前n项和,对数的运算性质
专题:等差数列与等比数列
分析:由已知得a4=2,从而log2a1+log2a2+…+log2a7=log2a47=7log2a4,由此能求出结果.
解答:
解:∵正项等比数列{an}中 a2•a6=4,
∴a4=2,
∴log2a1+log2a2+…+log2a7
=log2(a1×a2×…×a7)
=log2a47
=7log2a4
=7log22=7.
故选:C.
∴a4=2,
∴log2a1+log2a2+…+log2a7
=log2(a1×a2×…×a7)
=log2a47
=7log2a4
=7log22=7.
故选:C.
点评:本题考查对数值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
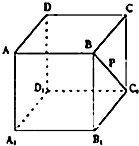 如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列结论:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的结论的个数是( )
如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列结论:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的结论的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
若在[2,4]上f(x)=loga(ax2-x)是增函数,则a取值范围是( )
| A、a>1 | ||
B、
| ||
C、
| ||
D、0<a<
|