题目内容
已知函数f(x)=
cos2x+sinx•cosx-
.
(Ⅰ)求函数f(x)的最小正周期T和函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)的对称中心为(x,0),求x∈[0,2π)的所有x的和.
| 3 |
| ||
| 2 |
(Ⅰ)求函数f(x)的最小正周期T和函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)的对称中心为(x,0),求x∈[0,2π)的所有x的和.
考点:两角和与差的正弦函数,正弦函数的单调性
专题:三角函数的图像与性质
分析:(Ⅰ)化简可得:f(x)=sin(2x+
)从而可求函数f(x)的最小正周期T和函数f(x)的单调递增区间;
(Ⅱ)令2x+
=kπ,k∈Z即可求出x的值,因为x∈[0,2π)故可求所有x的和.
| π |
| 3 |
(Ⅱ)令2x+
| π |
| 3 |
解答:
解:(I)∵由题得:f(x)=
cos2x+sinx•cosx-
=
•
+
sin2x-
=
cos2x+
sin2x=sin(2x+
).
∴f(x)=sin(2x+
),
∴T=
=π,
令-
+2kπ≤2x+
≤
+2kπ,k∈Z,
可得:递增区间为[-
+kπ,
+kπ],k∈Z;
(II)令2x+
=kπ,k∈Z,
可得:x=-
+
,k∈Z,
∵x∈[0,2π)∴k可取1,2,3,4.
∴所有满足条件的x的和为:
+
+
+
=
.
| 3 |
| ||
| 2 |
| 3 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
∴T=
| 2π |
| 2 |
令-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
可得:递增区间为[-
| 5π |
| 12 |
| π |
| 12 |
(II)令2x+
| π |
| 3 |
可得:x=-
| π |
| 6 |
| kπ |
| 2 |
∵x∈[0,2π)∴k可取1,2,3,4.
∴所有满足条件的x的和为:
| 2π |
| 6 |
| 5π |
| 6 |
| 8π |
| 6 |
| 11π |
| 6 |
| 13π |
| 3 |
点评:本题主要考察了两角和与差的正弦函数,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
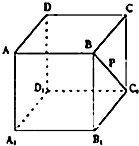 如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列结论:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的结论的个数是( )
如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列结论:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的结论的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知f(x)=
为偶函数,则y=loga(x2-4x-5)的单调递增区间为( )
|
| A、(-∞,-1) |
| B、(-∞,2) |
| C、(2,+∞) |
| D、(5,+∞) |