题目内容
3. 如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.
如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.(Ⅰ)证明:MN∥平面CB1D1;
(Ⅱ)证明:①A、P、O、C四点共面;②A、P、O三点共线.
分析 (Ⅰ)证明:MN∥B1D1,即可证明MN∥平面CB1D1;
(Ⅱ)①证明AA1与CC1共面,再证明P、O、∈平面AA1C1C,即可证明A、P、O、C四点共面;
②P是平面AA1C1C与平面AB1D1的公共点,故根据公理3,P在交线AO上,即可证明A、P、O三点共线.
解答 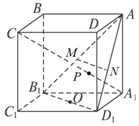 证明:(Ⅰ)∵M、N分别是AB1、AD1的中点,
证明:(Ⅰ)∵M、N分别是AB1、AD1的中点,
∴MN∥B1D1.(2分)
∵B1D1?平面CB1D1,MN?平面CB1D1,
∴MN∥平面CB1D1.(4分)
(Ⅱ)①∵ABCD-A1B1C1D1是正方体,∴AA1∥CC1,即AA1与CC1共面.(5分)
∵A1C1?平面AA1C1C,O∈A1C1,∴O∈平面AA1C1C.(6分)
∵A1C?平面AA1C1C,P∈A1C,∴P∈平面AA1C1C.(7分)
∴A、P、O、C∈平面AA1C1C,即A、P、O、C四点共面.(8分)
②∵AO是平面AA1C1C与平面AB1D1的交线,且P是平面AA1C1C与平面AB1D1的公共点,
故根据公理3,P在交线AO上.即A、P、O三点共线.(11分)
点评 本题考查线面平行的证明,考查平面的基本性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
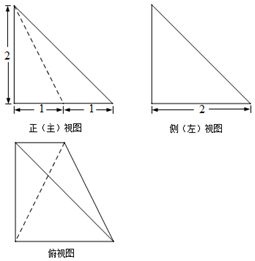

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
18.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
| A. | (1,+∞) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (0,1) |
8.已知f(x)是R上的奇函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+1),0≤x<1}\\{1-|x-3|,x≥1}\end{array}\right.$则函数y=f(x)+$\frac{1}{2}$的所有零点之和是( )
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 5-$\sqrt{2}$ | D. | $\sqrt{2}$-5 |
15.已知函数f(x)=$\left\{\begin{array}{l}sin\frac{x}{4}π,x>0\\ f({x+2}),x≤0\end{array}$,则f(-5)的值为( )
| A. | 0 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
12.已知$0<x<\frac{1}{3}$,则x(1-3x)取最大值时x的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |