题目内容
14.在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cosθ,θ∈[0,$\frac{π}{2}$].(1)求C的参数方程;
(2)设点D在C上,C在D处的切线与直线l:y=$\sqrt{3}$x+2垂直,根据(1)中你得到的参数方程,确定D的坐标.
分析 (1)根据极坐标方程求出C的普通方程,从而求出参数方程即可;(2)设D(1+cost,sint),结合题意得到直线GD与l的斜率相同,求出t的值,
解答 解:(1)由题意知:ρ=2cosθ,$θ∈[0,\frac{π}{2}]$,
所以ρ2=2ρcosθ,$θ∈[0,\frac{π}{2}]$,即x2+y2-2x=0,
可化为(x-1)2+y2=1,y∈[0,1],
可得C的参数方程为$\left\{\begin{array}{l}x=1+cost\\ y=sint\end{array}\right.$(t为参数,0≤t≤π).
(2)设D(1+cost,sint),
由(1)知C是以G(1,0)为圆心,1为半径的上半圆,
因为C在点D处的切线与l垂直,
所以直线GD与l的斜率相同,
∴$\frac{sint-0}{(1+cost)-1}=\sqrt{3}$,解得$tant=\sqrt{3}$,即$t=\frac{π}{3}$,
故D的直角坐标为$(1+cos\frac{π}{3},sin\frac{π}{3})$,
即$(\frac{3}{2},\frac{{\sqrt{3}}}{2})$.
点评 本题考查了参数方程、普通方程以及极坐标方程的转化,考查直线的斜率问题,是一道中档题、

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
2.抛物线y2=2x的焦点到准线的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
9.《庄子•天下篇》中记述了一个著名命题:“一尺之锤,日取其半,万世不竭”.反映这个命题本质的式子是( )
| A. | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$ | B. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$<1 | ||
| C. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1 | D. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$>1 |
4.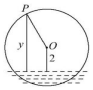 如图一半径为3米的水轮,水轮的圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2则有( )
如图一半径为3米的水轮,水轮的圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2则有( )
 如图一半径为3米的水轮,水轮的圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2则有( )
如图一半径为3米的水轮,水轮的圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2则有( )| A. | ω=$\frac{2π}{15}$,A=3 | B. | ω=$\frac{2π}{15}$,A=5 | C. | ω=$\frac{15π}{2}$,A=5 | D. | ω=$\frac{15π}{2}$,A=3 |

 如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.
如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.