题目内容
11．某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）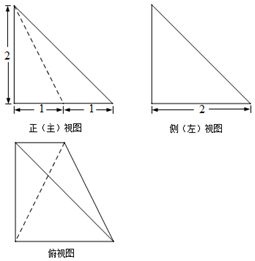
| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | $\frac{8}{3}$ |
分析 由已知中的三视图可得：该几何体是一个以俯视图中右下角的三角形为底面的三棱锥，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得：该几何体是一个以俯视图中左上角的三角形为底面的三棱锥，
其直观图如下图所示：
其底面面积S=$\frac{1}{2}$×2×2=2，
高h=2，
故棱锥的体积V=$\frac{1}{3}Sh$=$\frac{4}{3}$，
故选：B．
点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
智能训练练测考系列答案
相关题目
1．不等式组$\left\{\begin{array}{l}{2x+y-3≤0}\\{3x-y+3≥0}\\{x-2y+1≤0}\end{array}\right.$的解集记为D，有下面四个命题：
p1：?（x，y）∈D，2x+3y≥-1；
p2：?（x，y）∈D，2x-5y≥-3；
p3：?（x，y）∈D，$\frac{y-1}{2-x}$≤$\frac{1}{3}$；
p4：?（x，y）∈D，x2+y2+2y≤1．
其中的真命题是（ ）
p1：?（x，y）∈D，2x+3y≥-1；
p2：?（x，y）∈D，2x-5y≥-3；
p3：?（x，y）∈D，$\frac{y-1}{2-x}$≤$\frac{1}{3}$；
p4：?（x，y）∈D，x2+y2+2y≤1．
其中的真命题是（ ）
| A． | p1，p2 | B． | p2，p3 | C． | p2，p4 | D． | p3，p4 |
2．抛物线y2=2x的焦点到准线的距离为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | 3 |
如图，ABCD-A1B1C1D1是正方体，O、M、N分别是B1D1、AB1、AD1的中点，直线A1C交平面AB1D1于点P．
20．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入了部分数据，如表：
（1）请将上表数据补充完整，并直接写出函数f（x）的解析式；
（2）将函数y=f（x）的图象向左平移$\frac{π}{4}$个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）的单调递减区间．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin（ωx+φ） | 0 | 2 | -2 | 0 |
（2）将函数y=f（x）的图象向左平移$\frac{π}{4}$个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）的单调递减区间．