题目内容
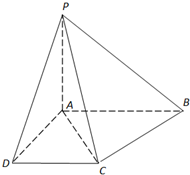 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.(1)求证:BC⊥平面PAC;
(2)求二面角A-PC-D的平面角α的正弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)首先利用矩形和勾股定理求出线线垂直,最后利用线面垂直的判定证明结论.
(2)根据(1)的结论,进一步求出点D到PC的距离,点D到平面PAC的距离,最后求出结果.
(2)根据(1)的结论,进一步求出点D到PC的距离,点D到平面PAC的距离,最后求出结果.
解答:
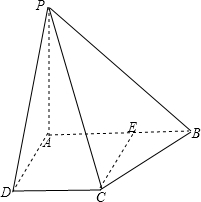
(1)证明:在直角梯形ABCD中,过C作CE⊥AB于点E,
则四边形ADCE为矩形
∴AE=DC=1,又AB=2,
∴BE=1,在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB=
∴AD=CE=1,
则AC=
=
,
AC2+BC2=AB2
∴BC⊥AC又
∵PA⊥平面ABCD
∴PA⊥BC,PA∩AC=A
∴BC⊥平面PAC
(2)解:∵PA⊥平面AC,CD⊥AD
∴CD⊥平面PAD
∴CD⊥PD,
又PA=AD=1,
AC=
∴PC=
PD=
∴点D到PC的距离h′=
=
在三棱锥P-ACD中,S△ADC=
•CD•AD=
,
S△PAC=
•AC•PA=
,
VP-ACD=VD-PAC;
∴点D到平面PAC的距离h=
=
=
∴sinα=
=
则四边形ADCE为矩形
∴AE=DC=1,又AB=2,
∴BE=1,在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB=
| 2 |
∴AD=CE=1,
则AC=
| AD2+DC2 |
| 2 |
AC2+BC2=AB2
∴BC⊥AC又
∵PA⊥平面ABCD
∴PA⊥BC,PA∩AC=A
∴BC⊥平面PAC
(2)解:∵PA⊥平面AC,CD⊥AD
∴CD⊥平面PAD
∴CD⊥PD,
又PA=AD=1,
AC=
| 2 |
∴PC=
| 3 |
| 2 |
∴点D到PC的距离h′=
| S△PCD | ||
|
| ||
|
在三棱锥P-ACD中,S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PAC=
| 1 |
| 2 |
| ||
| 2 |
VP-ACD=VD-PAC;
∴点D到平面PAC的距离h=
| VP-ACD | ||
|
| ||
|
| 1 | ||
|
∴sinα=
| h |
| h′ |
| ||
| 2 |

点评:本题考查的知识要点:线面垂直的判定定理,利用体积的关系求夹角,属于中等题型.

练习册系列答案
相关题目
正方体ABCD-A1B1C1D1中,M,N分别是CC1,BC的中点,则过A、M、N三点的正方体ABCD-A1B1C1D1的截面形状是( )
| A、平行四边形 | B、直角梯形 |
| C、等腰梯形 | D、以上都不对 |
若一个三角形,采用斜二测画法作出其直观图,则其直观图的面是原三角形面积的( )
A、
| ||||
| B、2倍 | ||||
C、
| ||||
D、
|
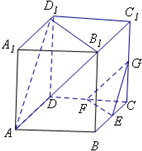 如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.