题目内容
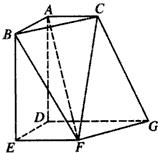 如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.
如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.考点:二面角的平面角及求法
专题:空间角
分析:在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,根据二面角的平面角的定义可知∠MNF是所求二面角的平面角,在直角三角形MNF中,先求出此角的正切值,然后再求出余弦值.
解答:

 解:∵四边形EFGD是直角梯形,AD⊥面DEFG
解:∵四边形EFGD是直角梯形,AD⊥面DEFG
∴DE⊥DG,DE⊥AD,即DE⊥面ADGC,
∵MF∥DE,且MF=DE,∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴CD=CG=
,∴cos∠DGC=
=
=
∴sin∠DGC=
,∴MN=MG•sin∠DGC=
在直角三角形MNF中,MF=2,MN=
∴tan∠MNF=
=
=
,cos∠MNF=
故面ADGC与面BCGF所组成的二面角余弦值为
.

 解:∵四边形EFGD是直角梯形,AD⊥面DEFG
解:∵四边形EFGD是直角梯形,AD⊥面DEFG∴DE⊥DG,DE⊥AD,即DE⊥面ADGC,
∵MF∥DE,且MF=DE,∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴CD=CG=
| 5 |
| GC2+GD2-CD2 |
| 2×GC×GD |
| 5+4-5 | ||
2×
|
| ||
| 5 |
∴sin∠DGC=
2
| ||
| 5 |
2
| ||
| 5 |
在直角三角形MNF中,MF=2,MN=
2
| ||
| 5 |
∴tan∠MNF=
| MF |
| MN |
| 2 | ||||
|
| 5 |
| ||
| 6 |
故面ADGC与面BCGF所组成的二面角余弦值为
| ||
| 6 |
点评:本题主要考查相交平面所成二面角以及空间几何体的几何量的计算等知识,考查空间想象能力和推理论证能力、利用综合法解决立体几何问题的能力.也可以利用向量法求解.

练习册系列答案
相关题目
在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=3,则直线A1C与平面ABC1D1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
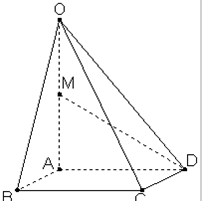 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.