题目内容
已知θ∈(π,
π),且cosθ=-
,则tanθ= .
| 3 |
| 2 |
| ||
| 5 |
考点:同角三角函数基本关系的运用
专题:
分析:依题意,可求得sinθ=-
=-
,从而可求得tanθ.
| 1-cos2θ |
2
| ||
| 5 |
解答:
解:∵cosθ=-
,θ∈(π,
π),
∴sinθ=-
=-
,
∴tanθ=
=2,
故答案为:2.
| ||
| 5 |
| 3 |
| 2 |
∴sinθ=-
| 1-cos2θ |
2
| ||
| 5 |
∴tanθ=
| sinθ |
| cosθ |
故答案为:2.
点评:本题考查同角三角函数基本关系的运用,属于基础题.

练习册系列答案
相关题目
已知向量
=(-1,-2,1),
=(2,x,3),若
⊥(
+
),则实数x的值为( )
| a |
| b |
| a |
| a |
| b |
A、-
| ||
| B、3 | ||
C、
| ||
D、
|
已知f(x)=log2x,则f(
)=( )
| 1 |
| 2 |
| A、2 | B、1 |
| C、(-1,3) | D、(-1,3) |
设集合M={(x,y)|y=2x2-x-1},N={y|y=2x2-x-1},则M∩N( )
| A、∅ | B、M | C、N | D、不存在 |
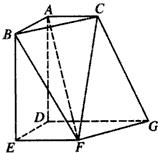 如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.
如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值. 执行如图所示的框图,若输入N=6,则输出的数S等于
执行如图所示的框图,若输入N=6,则输出的数S等于