题目内容
若3a=5b=15,则
+
= .
| 1 |
| a |
| 1 |
| b |
考点:指数式与对数式的互化
专题:函数的性质及应用
分析:由a=log315,b=log515,得
=log153,
=log155,由此能求出
+
.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
解答:
解:∵3a=5b=15,
∴a=log315,b=log515,
∴
=log153,
=log155,
∴
+
=log153+log155=log1515=1.
故答案为:1.
∴a=log315,b=log515,
∴
| 1 |
| a |
| 1 |
| b |
∴
| 1 |
| a |
| 1 |
| b |
故答案为:1.
点评:本题考查代数和的求和,是基础题,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
相关题目
高三毕业时,甲、乙、丙三位同学站成一排照相留念,则甲、丙两人相邻的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数g(x)满足g(x+3)=g(-x),若f(x)在(-2,0)∪(0.2)上为偶函数,且f(x)=
,则g(-2015)=( )
|
| A、0 | ||
| B、-1 | ||
C、
| ||
D、-
|
已知向量
=(-1,-2,1),
=(2,x,3),若
⊥(
+
),则实数x的值为( )
| a |
| b |
| a |
| a |
| b |
A、-
| ||
| B、3 | ||
C、
| ||
D、
|

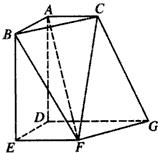 如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.
如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.