题目内容
如果向量
=(4,-2),
=(x,1),且
,
共线,那么实数x= .
| a |
| b |
| a |
| b |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:利用向量共线定理即可得出.
解答:
解:∵
∥
,
∴-2x-4=0,
解得x=-2.
故答案为:-2.
| a |
| b |
∴-2x-4=0,
解得x=-2.
故答案为:-2.
点评:本题考查了向量共线定理,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
函数f(x)=
+ln(x+1)的定义域为( )
| 1 | ||
|
| A、(2,+∞) |
| B、(-1,2)∪(2,+∞) |
| C、(-1,2) |
| D、(-1,2] |
若cosa=-
,且a是第三象限角,则tana=( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
集合M={x|(x-1)(x-2)<0},N={x|x<a},若M⊆N,则实数a的取值范围是( )
| A、[2,+∞) |
| B、(2,+∞) |
| C、[1,+∞) |
| D、(1,+∞) |
已知2sinx=a-1,则a的取值范围( )
| A、-1<a<3 |
| B、-1≤a≤3 |
| C、0<a<2 |
| D、0≤a≤2 |
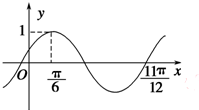 函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<