题目内容
已知直线l:
(t为参数且t∈R)与曲线C:
(α是参数且α∈[0,2π)),则直线l与曲线C的交点坐标为 .
|
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把直线l的参数方程化为普通方程,曲线C的参数方程化为普通方程,两方程联立,即可求出直线l与曲线C的交点坐标.
解答:
解:直线l:
(t为参数且t∈R),
化为普通方程是:2x+y-5=0;
曲线C:
(α是参数且α∈[0,2π)),
化为普通方程是:y=2x2+1(其中-1≤x≤1);
由
,
解得x=1,y=3;
∴直线l与曲线C的交点坐标为(1,3).
故答案为:(1,3).
|
化为普通方程是:2x+y-5=0;
曲线C:
|
化为普通方程是:y=2x2+1(其中-1≤x≤1);
由
|
解得x=1,y=3;
∴直线l与曲线C的交点坐标为(1,3).
故答案为:(1,3).
点评:本题考查了参数方程的应用问题,解题时可以把参数方程化为普通方程来解答,要注意互化前后范围是否一致,是基础题.

练习册系列答案
相关题目
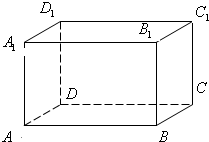 如图,长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长分别为AD=3,AA1=4,AB=5,则从A点沿表面到C1的最短距离为( )
如图,长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长分别为AD=3,AA1=4,AB=5,则从A点沿表面到C1的最短距离为( )A、5
| ||
B、
| ||
C、4
| ||
D、3
|
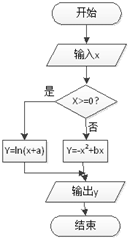 小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0.
小明在做一道函数题时,不小心将一个分段函数的解析式污染了一部分,但是已知这个函数的程序框图如图所示,且当分别输入数据-2,0 时,输出的结果都是0. 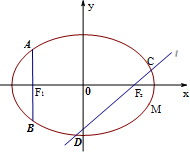 已知椭圆E:
已知椭圆E: