题目内容
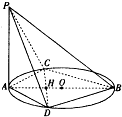 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.(Ⅰ)求证:PB⊥CD;
(Ⅱ)若PB与圆O所在平面所成角为
| π |
| 4 |
| 2π |
| 3 |
考点:用空间向量求平面间的夹角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)要证明线线垂直,重点要根据线面垂直进行转化,即要证明PB⊥CD只要能证明CD⊥平面PAB即可,进一步找到CD⊥平面PAB的条件.
(Ⅱ)要求二面角C-PB-D的大小的余弦值,直接使用几何法较为困难,可以通过建立空间直角坐标系,利用平面的法向量以及向量的数量积来进行求解.
(Ⅱ)要求二面角C-PB-D的大小的余弦值,直接使用几何法较为困难,可以通过建立空间直角坐标系,利用平面的法向量以及向量的数量积来进行求解.
解答:
(Ⅰ)证明:
∵AB是圆O的直径
∴∠ACB=∠ADB=
,
∵AC=AD
∴Rt△ACB≌Rt△ADB
∴AB⊥CD
∵PA⊥圆O所在平面,CD在圆O所在平面内
∴PA⊥CD
∵PA∩AB=A
∴CD⊥平面PAB
∴PB⊥CD
(Ⅱ)建立如图所示的空间直角坐标系A-xyz:设PA=2
∵∠PBA是直线PB与圆O所在平面所成的平面角,且∠PBA=
∴AB=2
∵∠CAD=
,
∴∠CAB=∠DAB=
∴AC=1,CD=
∴D(
,
,0),C(-
,
,0),B(0,2,0),P(0,0,2)
=(
,-
,0),
=(-
,-
,0),
=(0,-2,2)
设平面PBD的法向量为:
=(x,y,z)
则
令x=
则
=(
,1,1)
同理解得平面PBC的法向量:
=(
,-1,-1)
设二面角C-PB-D的大小为θ
cosθ=
=
即二面角C-PB-D的大小的余弦值为
∵AB是圆O的直径
∴∠ACB=∠ADB=
| π |
| 2 |
∵AC=AD
∴Rt△ACB≌Rt△ADB
∴AB⊥CD
∵PA⊥圆O所在平面,CD在圆O所在平面内
∴PA⊥CD
∵PA∩AB=A
∴CD⊥平面PAB
∴PB⊥CD
(Ⅱ)建立如图所示的空间直角坐标系A-xyz:设PA=2
∵∠PBA是直线PB与圆O所在平面所成的平面角,且∠PBA=
| π |
| 4 |
∴AB=2
∵∠CAD=
| 2π |
| 3 |
∴∠CAB=∠DAB=
| π |
| 3 |
∴AC=1,CD=
| 3 |
∴D(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| BD |
| ||
| 2 |
| 3 |
| 2 |
| BC |
| ||
| 2 |
| 3 |
| 2 |
| BP |
设平面PBD的法向量为:
| V |
则
|
|
| 3 |
| V |
| 3 |
同理解得平面PBC的法向量:
| u |
| 3 |
设二面角C-PB-D的大小为θ
cosθ=
| ||||
|
|
| 1 |
| 5 |
即二面角C-PB-D的大小的余弦值为
| 1 |
| 5 |
点评:本题考查的知识点:直线与直线的垂直,直线与平面垂直的判定与性质以及线线垂直与线面垂直的互化,空间直角坐标系的建立,平面的法向量,向量的数量积,是高考的重点考查题型.

练习册系列答案
相关题目
