题目内容
已知函数f(x)=4sin(
+
)cos(
+
).
(Ⅰ)求函数f(x)的最小正周期和图象对称中心的坐标;
(Ⅱ)在△ABC中,设内角A,B,C的对边分别是a,b,c,如果c=1,f(C)=
+1,且△ABC的面积为
,求sinA+sinB+sinC的值.
| π |
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
(Ⅰ)求函数f(x)的最小正周期和图象对称中心的坐标;
(Ⅱ)在△ABC中,设内角A,B,C的对边分别是a,b,c,如果c=1,f(C)=
| 3 |
| ||
| 2 |
考点:余弦定理,两角和与差的余弦函数,两角和与差的正弦函数,三角函数的周期性及其求法
专题:解三角形
分析:(Ⅰ)利用两角和差的正弦公式、二倍角公式化简函数f(x)的解析式为2sin(x+
)+
,由此可得f(x)的周期及其图象的对称中心;
(Ⅱ)根据f(C)=
+1代入解析式求出角C的值,再由三角形的面积求出ab的值,由余弦定理得b2+a2=7,进而求出a+b的值,再根据定弦定理求出比值,变形后求出式子的值.
| 2π |
| 3 |
| 3 |
(Ⅱ)根据f(C)=
| 3 |
解答:
解:(Ⅰ)由题意得,f(x)=4sin(
+
)cos(
+
)
=4cos
(
cos
-
sin
)
=2
cos2
-2sin
cos
=
(1+cosx)-sinx
=2sin(x+
)+
,
所以函数f(x)的最小正周期为T=2π,
由x+
=kπ得,x=kπ-
(k∈Z),
则函数的图象对称中心的坐标是(kπ-
,
)(k∈Z);
(Ⅱ)因为f(C)=
+1,
所以2sin(C+
)+
=
+1,化简得sin(C+
)=
,
因为0<C<π,所以
<C+
<
,
所以C+
=
,解得C=
,
又△ABC的面积为
,所以
absin
=
,
解得ab=2
,①
由余弦定理得,c2=b2+a2-2abcos
=1,
得b2+a2=7,②,
由①②得,a+b=
=
=
=2+
,
由正弦定理得,
=
=
=
=2,
则
=
,
解得,sinA+sinB+sinC=
(a+b+c)=
.
| π |
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
=4cos
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
=2
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=
| 3 |
=2sin(x+
| 2π |
| 3 |
| 3 |
所以函数f(x)的最小正周期为T=2π,
由x+
| 2π |
| 3 |
| 2π |
| 3 |
则函数的图象对称中心的坐标是(kπ-
| 2π |
| 3 |
| 3 |
(Ⅱ)因为f(C)=
| 3 |
所以2sin(C+
| 2π |
| 3 |
| 3 |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
因为0<C<π,所以
| 2π |
| 3 |
| 2π |
| 3 |
| 5π |
| 3 |
所以C+
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
又△ABC的面积为
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
解得ab=2
| 3 |
由余弦定理得,c2=b2+a2-2abcos
| π |
| 6 |
得b2+a2=7,②,
由①②得,a+b=
| (a+b2) |
| a2+2ab+b2 |
7+2
|
| 3 |
由正弦定理得,
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| 1 | ||
|
则
| sinA+sinB+sinC |
| a+b+c |
| 1 |
| 2 |
解得,sinA+sinB+sinC=
| 1 |
| 2 |
3+
| ||
| 2 |
点评:本题主要考查两角和差的正弦公式、二倍角公式的应用,三角函数的周期性及求法,正弦函数的对称中心,余弦定理、正弦定理的灵活应用,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目

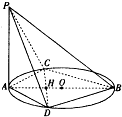 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.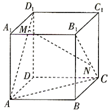 如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是
如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是