题目内容
11.某乳业公司生产甲、乙两种产品,需要A、B、C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如表所示:| 产品苜蓿草饲料 | A | B | C |
| 甲 | 4 | 8 | 3 |
| 乙 | 5 | 5 | 10 |
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
分析 (1)利用已知条件列出约束条件、画出可行域即可.
(2)利用可行域.求出目标函数的最优解,然后求解最值.
解答 解:(1)分别用x、y表示生产甲、乙两种产品的数量;由题意可得:
$\left\{\begin{array}{l}4x+5y≤200\\ 8x+5y≤360\\ 3x+10y≤300\\ x≥0,y≥0\end{array}\right.$;相应的平面区域如图:
(2)由约束条件的可行域可知z=2x+3y的最优解A,
由$\left\{\begin{array}{l}{4x+5y=200}\\{8x+5y=360}\end{array}\right.$解得A(40,8),
最大值zmax=104;
分别生产甲乙两种产品40吨;8吨,能够产出最大的利润,最大利润104万元.
点评 本题考查线性规划的简单应用,考查转化思想以及数形结合思想的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.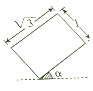 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )| A. | 2或3 | B. | 2$\sqrt{3}$或3 | C. | 1或3 | D. | 2或2$\sqrt{3}$ |
19.某几何体的三视图如图所示,则该几何体的体积等于( )


| A. | 8+8π | B. | 8+6π | C. | 6+8π | D. | 6+6π |
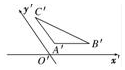 如图是三角形ABC的直观图,△ABC平面图形是直角三角形(填正三角形、锐角三角形、钝角三角形、直角三角形或者等腰三角形)
如图是三角形ABC的直观图,△ABC平面图形是直角三角形(填正三角形、锐角三角形、钝角三角形、直角三角形或者等腰三角形)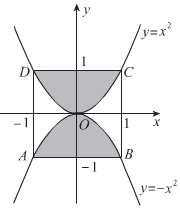 如图正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,求阴影区域的面积.
如图正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,求阴影区域的面积.