题目内容
20.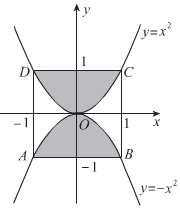 如图正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,求阴影区域的面积.
如图正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,求阴影区域的面积.
分析 根据积分的几何意义以及抛物线的对称性可知阴影部分的面积S.
解答 解:∵A(-1,-1),B(1,-1),C(1,1),D(-1,1),
根据积分的几何意义以及抛物线的对称性可知阴影部分的面积S=2${∫}_{-1}^{1}$(1-x2)dx=2(x-$\frac{1}{3}$x3)|${\;}_{-1}^{1}$
=2[(1-$\frac{1}{3}$)-(-1+$\frac{1}{3}$)]=2×$\frac{4}{3}$=$\frac{8}{3}$.
点评 本题主要考查了用积分求出阴影部分的面积,属于基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
10.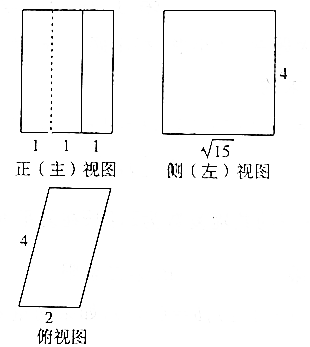 如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )
 如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )| A. | $\frac{8\sqrt{15}}{3}$ | B. | 8$\sqrt{15}$ | C. | $\frac{4\sqrt{15}}{3}$ | D. | 4$\sqrt{15}$ |
11.某乳业公司生产甲、乙两种产品,需要A、B、C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如表所示:
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
| 产品苜蓿草饲料 | A | B | C |
| 甲 | 4 | 8 | 3 |
| 乙 | 5 | 5 | 10 |
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
8.在△ABC中,内角A,B,C所对的边分别为a,b,c,A=$\frac{π}{4}$,b2-a2=c2,则tan C等于( )
| A. | 1 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
12.已知函数f(x)=$\left\{\begin{array}{l}{x+2,x>a}\\{{x}^{2}+5x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
9.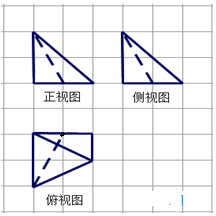 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
10.两条直线l1:2x+y+c=0,l2:x-2y+1=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 不能确定 |
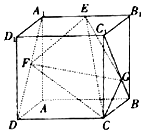 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.