题目内容
已知函数f(x)=
,则该函数的定义域为( )
| 2x-1 |
A、{x|x>
| ||
B、{x|x≥
| ||
C、{x|x>-
| ||
D、{x|x≥-
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件求函数的定义域即可,此题只需根式有意义即可.
解答:
解:解:要使函数有意义,则2x-1≥0,
即x≥
,
∴函数的定义域为[
,+∞)
故选:B.
即x≥
| 1 |
| 2 |
∴函数的定义域为[
| 1 |
| 2 |
故选:B.
点评:本题主要考查函数定义域的求法,要求熟练掌握函数成立的条件,比较基础.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
设f(x-2)=2x,则f(3)的值为( )
| A、64 | B、8 | C、16 | D、32 |
已知函数f(x)=ax2-4ax+c,(a<0),当f(m)≥f(0)时,实数m满足的取值范围是( )
| A、(-∞,0]∪[4,+∞) |
| B、[0,4] |
| C、(0,4) |
| D、(0,+∞) |
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A、命题p一定是真命题 |
| B、命题q一定是真命题 |
| C、命题q一定是假命题 |
| D、命题q可以是真命题也可以是假命题 |
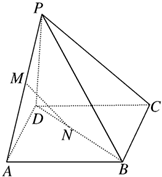 已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.
已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.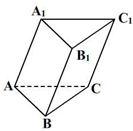 斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成45°角,求这个三棱柱的侧面积.
斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成45°角,求这个三棱柱的侧面积.