题目内容
17.已知集合A={x|x2-3x-4≥0},B={x|2<x<5},则A∩B=( )| A. | (1,5) | B. | [1,5) | C. | (4,5) | D. | [4,5) |
分析 求解一元二次不等式化简集合B,然后直接利用交集的运算求解.
解答 解:集合A={x|x2-3x-4≥0}=(-∞,-1]∪[4,+∞),B={x|2<x<5}=(2,5),
则A∩B=[4,5),
故选:D
点评 本题考查交集及其运算,考查了一元二次不等式的解法,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若抛物线y2=ax的焦点到其准线的距离是2,则a=( )
| A. | ±1 | B. | ±2 | C. | ±4 | D. | ±8 |
2.城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表:
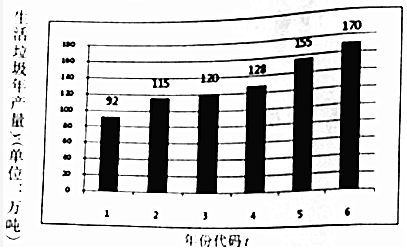
注1:年份代码1~6分别对应年份2011~2016
注2:参与度=$\frac{参加垃圾分类人数}{调查人数}$×100%
参与度的年增加值=年末参与度-年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为$\widehat{y}$=14.8t+$\widehat{a}$,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题:
①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?

| 2016年初 | 2016年末 | |
| 社区A | 539 | 568 |
| 社区B | 543 | 585 |
| 社区C | 568 | 600 |
| 社区D | 496 | 513 |
注2:参与度=$\frac{参加垃圾分类人数}{调查人数}$×100%
参与度的年增加值=年末参与度-年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为$\widehat{y}$=14.8t+$\widehat{a}$,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题:
①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?
6.已知公比q≠1的等比数列{an}前n项和Sn,a1=1,S3=3a3,则S5=( )
| A. | 1 | B. | 5 | C. | $\frac{31}{48}$ | D. | $\frac{11}{16}$ |
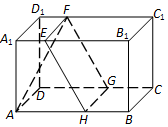 如图,在长方体ABCD-A1B1C1D1中,AB=8,BC=5,AA1=4,平面α截长方体得到一个矩形EFGH,且A1E=D1F=2,AH=DG=5.
如图,在长方体ABCD-A1B1C1D1中,AB=8,BC=5,AA1=4,平面α截长方体得到一个矩形EFGH,且A1E=D1F=2,AH=DG=5.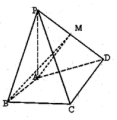 在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.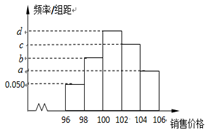 某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.
某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.