题目内容

若a 
1
2
＜（3-2a） 
1
2
，则实数a的取值范围为
 
．
考点：指数函数的图像与性质
专题：分类讨论,不等式的解法及应用
分析：根据题意，应满足
a＞0
3-2a＞0
a≠1
，求出a的取值范围，再讨论a在该范围内使不等式成立的a的取值范围．
解答： 解：根据题意得，
a＞0
3-2a＞0
a≠1
；
即0＜a＜1，或1＜a＜
3
2
；
当0＜a＜1时，3-2a＞1，
不等式a 
1
2
＜（3-2a） 
1
2
化为a＜3-2a，
解得a＜1，∴0＜a＜1；
当1＜a＜
3
2
时，1＞3-2a＞0，
不等式a 
1
2
＜（3-2a） 
1
2
化为a＜3-2a，
解得a＜1，∴a∈∅；
综上，a的取值范围是{a|0＜a＜1}．
故答案为：{a|0＜a＜1}．
点评：本题考查了不等式的解法与应用问题，解题时应根据不等式的特点进行化简和讨论，从而求出不等式成立的a的取值范围，是基础题．
练习册系列答案
相关题目
在正项等比数列{an}中，a1和a19为方程x2-10x+16=0的两根，则a8•a12=
 
．
已知圆柱底面半径为r，O是上底面圆心，A、B是下底面圆周上两个不同的点，母线BC长为3．如图，若直线OA与BC所成角的大小为
π
6
，则r=
 
．
数列
5
4
，
10
9
，
17
a+b
，
a-b
25
，…中，有序数对（a，b）可以是
 
．
已知数列{an}：a1，a2，…，an（n≥3），令集合T={x|x=ai+aj，1≤i＜j≤n}，card（T）表示集合T中元素个数．若{an}满足：an+1-an=c（c为常数，n≥1），则card（T）=
 
．
（举例说明：若{an}：1，2，3，4，则T={3，4，5，6，7}，card（T）=5．）
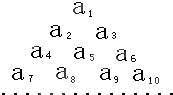已知数列{an}是首项为1，公差为2的等差数列，将数列{an}中的各项排成如图所示的一个三角形数表，记A（i，j）表示第i行从左至右的第j个数，例如A（4，3）=a9，则A（10，4）=
 
．
关于函数f（x）=cos（2x-
π
3
）+sin（2x+
π
6
）有下列命题：
①y=f（x）是以π为最小正周期的周期函数；
②y=f（x）的一条对称轴为x=-
π
3
；
③y=f（x）在区间（
π
6
，
2π
3
）上单调递减；
④将函数y=2cos2x的图象向左平移
π
6
个单位后，将与已知函数的图象重合．
其中正确命题的序号是
 
．（注：把你认为正确的命题的序号都填上）
已知函数y=alnx-x+1的图象在x=1处的切线与直线x+2y-1=0垂直，则实数a的值为
 
．
两等差数列{an}和{bn}，前n项和分别为Sn，Tn，且
Sn
Tn
=
7n+2
n+3
，则
a11
b11
等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网