题目内容
已知圆柱底面半径为r，O是上底面圆心，A、B是下底面圆周上两个不同的点，母线BC长为3．如图，若直线OA与BC所成角的大小为| π |
| 6 |
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：过A作与BC平行的母线AD，由异面直线所成角的概念得到∠OAD=
．在直角三角形ODA中，直接由tan
=
得到答案．
| π |
| 6 |
| π |
| 6 |
| r |
| l |
解答：
解：如图，过A作与BC平行的母线AD，连接OD，
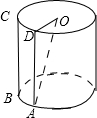
则∠OAD为直线OA与BC所成的角，
∴∠OAD=
．
在直角三角形ODA中，tan
=
=
=
，
解得；r=
，
故答案为：
则∠OAD为直线OA与BC所成的角，
∴∠OAD=
| π |
| 6 |
在直角三角形ODA中，tan
| π |
| 6 |
| r |
| l |
| r |
| 3 |
| ||
| 3 |
解得；r=
| 3 |
故答案为：
| 3 |
点评：本题考查了异面直线所成的角，考查了直角三角形的解法，是基础题．
练习册系列答案
相关题目
将全体正整数排成一个三角形数阵：按照以上排列的规律，第n行（n≥2）从左向右的第2个数为