Question

已知关于x的方程x²+（1+a）x+1+a+b=0（a，b∈R）的两根分别为x₁、x₂，且0＜x₁＜1＜x₂，则

b

a

的取值范围是（　　）

• A、[-2，-

  1

  2

  ]
• B、（-2，-

  1

  2

  ]
• C、[

  1

  2

  ，2]
• D、(

  1

  2

  ，2)

Answer 1

考点：函数的零点与方程根的关系

专题：数形结合,不等式的解法及应用

分析：先根据方程根的分布得出关于a，b的约束条件，再由约束条件画出可行域，明确目标函数的几何意义求最值即可．

解答： 解：设f（x）=x²+（1+a）x+1+a+b，
由题意得：

f(0)＞0 f(1)＜0

∴

1+a+b＞0 2a+b+3＜0

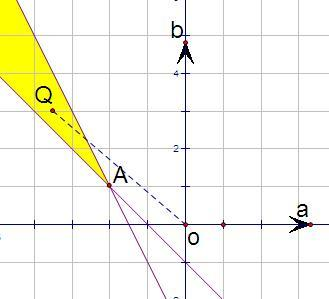
其对应的平面区域如图阴影示：
目标函数

b

a

表示阴影区域上一点与原点连线的斜率．
当连线OQ经过点A（-2，1）时，

b

a

最大是-

1

2

当连线OQ平行于直线2a+b+3=0时，直线OQ的斜率是-2，
∴

b

a

的取值范围是（-2，-

1

2

]．
故选B．

点评：本题考查的知识点是一元二次方程的根的分布与系数的关系，三个二次之间的关系，线性规划，构建不等式，明确目标函数的几何意义是关键．