Question

如图，四棱锥V-ABCD中，底面ABCD是边长为2的正方形，其它四个侧面都是侧棱长为

5

的等腰三角形，AC∩BD=O．
（1）求二面角V-AB-C的大小
（2）求点O到平面VAB的距离．

Answer 1

考点：二面角的平面角及求法,点、线、面间的距离计算

专题：计算题,证明题,空间角

分析：（1）取AB的中点E，连接EO，VE，VO，由正四棱锥的性质易得∠VEO为二面角V-AB-C的平面角，在Rt△VEO中分别求出OE、VE的长，可得cos∠VEO的值，从而得到∠VEO的大小，即得二面角V-AB-C的大小；
（2）设点O到平面VAB的距离为h，根据三棱锥O-VAB和体积等于三棱锥V-OAB的体积，得到S_△VAB•h=S_△OAB•VO，将题中的数据代入，可得h=

3

2

，即得点O到平面VAB的距离的大小．

解答： 解：（1）取AB的中点E，连接EO，VE，VO，则由题意可知VE⊥AB且OE⊥AB，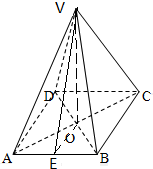
∴∠VEO为二面角V-AB-C的平面角，
∵VA=VB=VC=VD=

5

，O是底面正方形ABCD的中心，
∴VO⊥平面ABCD
Rt△VEO中，OE=

1

2

BC=1，VE=

VA2-AE2

=

5-1

=2
∴cos∠VEO=

OE

VE

=

1

2

，可得∠VEO=60°
∴二面角V-AB-C的大小为60°
（2）设点O到平面VAB的距离为h，
则由V_O-VAB=V_V-OAB，得S_△VAB•h=S_△OAB•VO
∵S_△VAB=

1

2

×AB×VE=2，S_△OAB=

1

2

×AB×EO=1，VO=

22-12

=

3

∴2×h=1×

3

，得h=

3

2

即点O到平面VBC的距离为

3

2

．

点评：本题给出正四棱锥，求侧面与底面所成角的大小，并求底面中心到一个侧面的距离，着重考查了二面角的平面角及求法和点到平面距离求法等知识，属于中档题．