已知:在平面Rt△ABC.∠C=90°.动点P满足|PC|+|CB|=|PA|+|AB|.则点P的轨迹是( )A．椭圆B．双曲线C．双曲线的一支D．抛物线题目和参考答案——青夏教育精英家教网—

题目内容

3．已知：在平面Rt△ABC，∠C=90°，动点P满足|PC|+|CB|=|PA|+|AB|，则点P的轨迹是（　　）

A．

椭圆

B．

双曲线

C．

双曲线的一支

D．

抛物线

分析动点P满足|PC|+|CB|=|PA|+|AB|，可得|PC|-|PA|=|AB|-|CB|＜|AC|，即可求出点P的轨迹．

解答解：∵动点P满足|PC|+|CB|=|PA|+|AB|，
∴|PC|-|PA|=|AB|-|CB|＜|AC|，
∴点P的轨迹是双曲线的一支，
故选：C．

点评本题考查轨迹方程，考查双曲线的定义，比较基础．

练习册系列答案

中学生英语随堂演练及单元要点检测题系列答案

14．已知全集U=R，集合A={x|x＜-4，或x＞1}，B={x|-3≤x-1≤2}，
（1）求A∩B，（∁_UA）∪（∁_UB）；
（2）若集合M={x|2a≤x≤2a+1}是集合A的子集，求实数a的取值范围．

11．若用“五点法”画函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π）的图象，其五点如下表：

x	$\frac{π}{2}$	2π	$\frac{7π}{2}$	5π	$\frac{13π}{2}$
y	0	2	0	-2	0

（1）求函数f（x）的解析式；
（2）设g（x）=Acos（ωx+φ），若关于x的方程g（x）+λ=0在[π，7π]内恰有两个不同的解α，β，求实数λ的取值范围，并求α+β的值．

18．P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1上在第一象限内的一点，过P作实轴的垂线，垂足为M（10，0），又过M作圆x²+y²=a²的切线，切点为Q，若cos∠MOQ=$\frac{3}{5}$，求双曲线的方程和点P的坐标．

8．一个三棱锥三视图如图所示，则该三棱锥的外接球的表面积为（　　）

15．已知奇函数f（x）=$\frac{a•{2}^{x}-2+a}{{2}^{x}+1}$．
（1）求a的值；
（2）求函数f（x）的值域；
（3）若对任意t∈（-1，0]，不等式f（t²-mt+7）+f（t²+5t-m）＞0恒成立，求m的取值范围．

14．

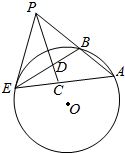如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE，BE，∠APE的平分线与AE，BE分别交于点C，D．
（1）求证：$\frac{DB}{DE}$=$\frac{PD}{PC}$；
（2）若∠PCE=2∠AEB，求∠PDB的大小．

15．函数y=cos²x+sinx（-$\frac{π}{6}$≤x≤$\frac{π}{6}$）的最大值与最小值之和为（　　）

试题分类