题目内容
18．P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1上在第一象限内的一点，过P作实轴的垂线，垂足为M（10，0），又过M作圆x2+y2=a2的切线，切点为Q，若cos∠MOQ=$\frac{3}{5}$，求双曲线的方程和点P的坐标．分析 连OQ，则OQ⊥MQ，cos∠MOQ=$\frac{|OQ|}{|OM|}$=$\frac{a}{10}$=$\frac{3}{5}$，可以求出a，即可求双曲线的方程和点P的坐标．
解答 解：连OQ，则OQ⊥MQ，cos∠MOQ=$\frac{|OQ|}{|OM|}$=$\frac{a}{10}$=$\frac{3}{5}$，所以a=6
所以双曲线的方程为$\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{9}$=1
设 P（10，y0），代入方程，得$\frac{100}{36}$-$\frac{{{y}_{0}}^{2}}{9}$=1，解得y0=4，（y0=-4舍），即P（10，4）．
点评 本题考查椭圆方程，考查直线与圆的位置关系，属于中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8．某学生四次模拟考试时，其英语作文的减分情况如下表：
显然所减分数y与模拟考试次数x之间有较好的线性相关关系，参考公式：
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，$\overline{x}$=$\frac{1}{n}$$\sum_{i=1}^{n}$xi，$\overline{y}$=$\frac{1}{n}$$\sum_{i=1}^{n}$yi
则其回归线性方程为$\widehat{y}$=-0.7x+5.25．
| 考试次数x | 1 | 2 | 3 | 4 |
| 所减分数y | 4.5 | 4 | 3 | 2.5 |
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，$\overline{x}$=$\frac{1}{n}$$\sum_{i=1}^{n}$xi，$\overline{y}$=$\frac{1}{n}$$\sum_{i=1}^{n}$yi
则其回归线性方程为$\widehat{y}$=-0.7x+5.25．
9．已知函数f（x）=x+x3，x1，x2，x3∈R，x1+x2＞0，x2+x3＞0，x3+x1＞0，那么f（x1）+f（x2）+f（x3）的值（ ）
| A． | 一定大于0 | B． | 等于0 | C． | 一定小于0 | D． | 正负都有可能 |
3．已知：在平面Rt△ABC，∠C=90°，动点P满足|PC|+|CB|=|PA|+|AB|，则点P的轨迹是（ ）
| A． | 椭圆 | B． | 双曲线 | C． | 双曲线的一支 | D． | 抛物线 |
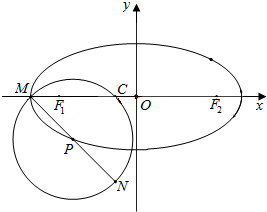已知椭圆E的方程：$\frac{x^2}{100}+\frac{y^2}{25}=1$，P为椭圆上的一点（点P在第三象限上），圆P 以点P为圆心，且过椭圆的左顶点M与点C（-2，0），直线MP交圆P与另一点N．