题目内容
曲线y=
x5上点M处的切线与直线y=3-x垂直，则切线方程为（ ）
| 1 |
| 5 |
| A、5x-5y-4=0 |
| B、5x+5y-4=0 |
| C、5x+5y-4=0或5x+5y+4=0 |
| D、5x-5y-4=0或5x-5y+4=0 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：由已知得y′=x4，曲线y=
x5上点M处的切线的斜率k=1，由此能求出切线方程．
| 1 |
| 5 |
解答：
解：∵y=
x5，∴y′=x4，
∵曲线y=
x5上点M处的切线与直线y=3-x垂直，
∴曲线y=
x5上点M处的切线的斜率k=1，
∴k=x4，∴x=1或x=-1
y=
或y=-
，
∴切线方程为y=x-
或y=x+
，
整理，得：5x-5y-4=0或5x-5y+4=0．
故选：D．
| 1 |
| 5 |
∵曲线y=
| 1 |
| 5 |
∴曲线y=
| 1 |
| 5 |
∴k=x4，∴x=1或x=-1
y=
| 1 |
| 5 |
| 1 |
| 5 |
∴切线方程为y=x-
| 4 |
| 5 |
| 4 |
| 5 |
整理，得：5x-5y-4=0或5x-5y+4=0．
故选：D．
点评：本题考查切线方程的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
相关题目
若y=（x+1）（x+2）（x-1），则y′=（ ）
| A、x3+2x2-x-2 |
| B、3x2+4x-1 |
| C、3x2+4x-2 |
| D、3x2+4x-3 |
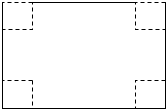如图，一矩形铁皮的长为8cm，宽为5cm，在四个角上截去四个相同的小正方形，制成一个无盖的小盒子，问小正方形的边长为