题目内容
已知定义在R上的函数f(x)=2x+
(1)判断f(x)为奇偶性;
(2)证明f(x)函数在[0,+∞)上单调递增.
| 1 |
| 2x |
(1)判断f(x)为奇偶性;
(2)证明f(x)函数在[0,+∞)上单调递增.
考点:命题的真假判断与应用,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用函数奇偶性的定义判定f(-x)是等于f(x),还是等于-f(x)即可.
(2)?0≤x1<x2,利用指数函数的单调性只要证明f(x1)-f(x2)<0即可.
(2)?0≤x1<x2,利用指数函数的单调性只要证明f(x1)-f(x2)<0即可.
解答:
解:(1)?x∈R,则f(-x)=2-x+
=
+2x=f(x),
∴函数f(x)是偶函数.
(2)?0≤x1<x2,则f(x1)-f(x2)=2x1+
-(2x2+
)=(2x1-2x2)
.
∵0≤x1<x2,
∴2x1<2x2,2x1+x2>20=1,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2).
∴f(x)函数在[0,+∞)上单调递增.
| 1 |
| 2-x |
| 1 |
| 2x |
∴函数f(x)是偶函数.
(2)?0≤x1<x2,则f(x1)-f(x2)=2x1+
| 1 |
| 2x1 |
| 1 |
| 2x2 |
| 2x1+x2-1 |
| 2x1+x2 |
∵0≤x1<x2,
∴2x1<2x2,2x1+x2>20=1,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2).
∴f(x)函数在[0,+∞)上单调递增.
点评:本题考查了函数的奇偶性、单调性等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
下列说法错误的是( )
| A、若命题p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0 | ||
| B、若命题p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题. | ||
| C、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
D、“sinθ=
|
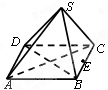 如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持
如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持