题目内容
4．若${（{1+mx}）^6}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_6}{x^6}$，且a1-a2+a3-a4+a5-a6=-63，则实数m的值为3或-1．分析 在所给的等式中，令x=0，可得a0=1．再令x=-1，可得a0-a1+a2 -a3 +a4 -a5 +a6=（1-m）6．再根据a1-a2+a3-a4+a5-a6=-63，求得 （1-m）6=64，由此求得m的值．
解答 解：∵${（{1+mx}）^6}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_6}{x^6}$，令x=0，可得a0=1．
再令x=-1，可得a0-a1+a2 -a3 +a4 -a5 +a6=（1-m）6．
∵a1-a2+a3-a4+a5-a6=-63，两边同时乘以-1，可得-a1+a2 -a3 +a4 -a5 +a6=63，
∴a0-a1+a2 -a3 +a4 -a5 +a6=64，即 （1-m）6=64，∴1-m=±2，∴m=3，或m=-1．
故答案为：3或-1．
点评 本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于中档题．
练习册系列答案
相关题目
14．
如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件）．若这两组数据的中位数相等，且平均值也相等，则x和y的值分别为（ ）
如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件）．若这两组数据的中位数相等，且平均值也相等，则x和y的值分别为（ ）| A． | 3，5 | B． | 5，5 | C． | 3，7 | D． | 5，7 |
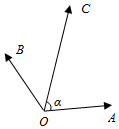如图，在同一个平面内，向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$的模分别为1，1，$\sqrt{2}$，$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为α，且tanα=7，$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为45°．若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m+n=3．
12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切，则C的离心率为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{1}{3}$ |