题目内容
14.在直角坐标系xOy中,直线l1的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=kt}\end{array}\right.$,(t为参数),直线l2的参数方程为$\left\{\begin{array}{l}{x=-2+m}\\{y=\frac{m}{k}}\end{array}\right.$,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)-$\sqrt{2}$=0,M为l3与C的交点,求M的极径.
分析 解:(1)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x-2)①与x=-2+ky②;联立①②,消去k可得C的普通方程为x2-y2=4;
(2)将l3的极坐标方程为ρ(cosθ+sinθ)-$\sqrt{2}$=0化为普通方程:x+y-$\sqrt{2}$=0,再与曲线C的方程联立,可得$\left\{\begin{array}{l}{x=\frac{3\sqrt{2}}{2}}\\{y=-\frac{\sqrt{2}}{2}}\end{array}\right.$,即可求得l3与C的交点M的极径为ρ=$\sqrt{5}$.
解答 解:(1)∵直线l1的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=kt}\end{array}\right.$,(t为参数),
∴消掉参数t得:直线l1的普通方程为:y=k(x-2)①;
又直线l2的参数方程为$\left\{\begin{array}{l}{x=-2+m}\\{y=\frac{m}{k}}\end{array}\right.$,(m为参数),
同理可得,直线l2的普通方程为:x=-2+ky②;
联立①②,消去k得:x2-y2=4,即C的普通方程为x2-y2=4(x≠±2);
(2)∵l3的极坐标方程为ρ(cosθ+sinθ)-$\sqrt{2}$=0,
∴其普通方程为:x+y-$\sqrt{2}$=0,
联立$\left\{\begin{array}{l}{x+y=\sqrt{2}}\\{{x}^{2}{-y}^{2}=4}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{3\sqrt{2}}{2}}\\{y=-\frac{\sqrt{2}}{2}}\end{array}\right.$,
∴ρ2=x2+y2=$\frac{18}{4}$+$\frac{2}{4}$=5.
∴l3与C的交点M的极径为ρ=$\sqrt{5}$.
点评 本题考查参数方程与极坐标方程化普通方程,考查函数与方程思想与等价转化思想的运用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | -80 | B. | -40 | C. | 40 | D. | 80 |
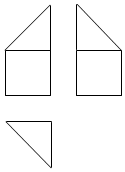 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
| A. | 12种 | B. | 18种 | C. | 24种 | D. | 36种 |