题目内容
16.已知函数f(x)=(4-x)ex-2,试判断是否存在m使得y=f(x)与直线3x-2y+m=0(m为确定的常数)相切?分析 求出f(x)的导数,可得切线的斜率,设g(x)=(3-x)ex-2,求出导数和单调区间,可得极值也为最值,假设存在m满足题意,由直线方程可得斜率大于最值,即可判断不存在.
解答 解:函数f(x)=(4-x)ex-2,
导数为f′(x)=(3-x)ex-2,
设g(x)=(3-x)ex-2,则g'(x)=(2-x)ex-2,
由x>2时,g'(x)<0,g(x)递减;x<2时,g'(x)>0,g(x)递增.
可推得g(x)极大值为g(2)=1,也为最大值.
假设y=f(x)与直线3x-2y+m=0(m为确定的常数)相切,
则切线的斜率为$\frac{3}{2}$,
由于切线的斜率的最大值为1.
所以$f'(x)=(3-x){e^{x-2}}=\frac{3}{2}$无解.
所以不存在m满足题意.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查存在性问题的解法,以及化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
6.若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m( )
| A. | 与a有关,且与b有关 | B. | 与a有关,但与b无关 | ||
| C. | 与a无关,且与b无关 | D. | 与a无关,但与b有关 |
11.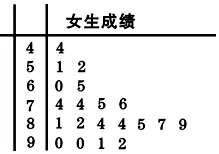 为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
(1)请根据题意,将2×2列联表补充完整;
(2)据此列联表判断,是否有90%的把握认为该学科成绩与性别有关?
附:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
 为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).(1)请根据题意,将2×2列联表补充完整;
| 优秀 | 非优秀 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
附:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
1.复数z满足$z({\sqrt{3}+i})=1-\sqrt{3}i$,则|z|=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
8.下面是关于复数z=2-i的四个命题:p1:|z|=5;p2:z2=3-4i;p3:z的共轭复数为-2+i;p4:z的虚部为-1,其中真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |