题目内容
方程xlg（x+2）=1有 个不同的实数根．
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：作出函数y=lg（x+2）与y=
（x＞-2）的图象，由图象的交点个数确定方程xlg（x+2）=1的解的个数．
| 1 |
| x |
解答：
解：∵xlg（x+2）=1，
∴lg（x+2）=
（x＞-2），
作图如下：
由图可知，y=lg（x+2）与y=
（x＞-2）有两个交点，
∴方程xlg（x+2）=1有2个不同的实数根，
故答案为：2．
∴lg（x+2）=
| 1 |
| x |
作图如下：
由图可知，y=lg（x+2）与y=
| 1 |
| x |
∴方程xlg（x+2）=1有2个不同的实数根，
故答案为：2．
点评：本题考查根的存在性及根的个数判断，作出函数y=lg（x+2）与y=
（x＞-2）的图象是关键，考查作图与转化能力，属于中档题．
| 1 |
| x |
练习册系列答案
相关题目
下列命题的否定是真命题的有（ ）
①△＜0时，方程ax2+bx+c=0（a≠0）无实根；
②存在一个整数m，使函数f（x）=x2+mx+2在[0，+∞）上不是单调函数；
③?x∈R，使x2+x+1≥0不成立．
①△＜0时，方程ax2+bx+c=0（a≠0）无实根；
②存在一个整数m，使函数f（x）=x2+mx+2在[0，+∞）上不是单调函数；
③?x∈R，使x2+x+1≥0不成立．
| A、0个 | B、1个 | C、2个 | D、3个 |
下列函数中，定义域为全体实数的是（ ）
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
在同一坐标系中，将曲线y=2sin3x变为曲线y=sinx的伸缩变换公式是（ ）
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
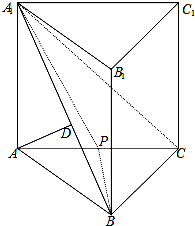如图，在直三棱柱ABC=A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上．