题目内容
设函数f(x)是定义在(0,+∞)上的增函数,对于任意正数x、y都有f(xy)=f(x)+f(y),且f(2)=1.若对于正数a、b满足f(2a+b)<2,求
的取值范围.
| b+2 |
| a+2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:先利用赋值法,求出f(4)=2,得到2a+b<4,且2a+b>0,由线性规化可得关于(a,b)可行域,可求式化为k=
=
,转化为可行域内的动点(a,b)与定点(-2,-2)连线的斜率可获得解
| b+2 |
| a+2 |
| b-(-2) |
| a-(-2) |
解答:
 解:令x=y=2,则f(2×2)=f(2)+f(2),
解:令x=y=2,则f(2×2)=f(2)+f(2),
∴f(4)=2f(2)=2×1=2.
∵f(2a+b)<2=f(4),f(x)是定义在(0,+∞)上的增函数
∴2a+b<4
∵2a+b>0,由线性规化可得关于(a,b)可行域,
∵设k=
=
,
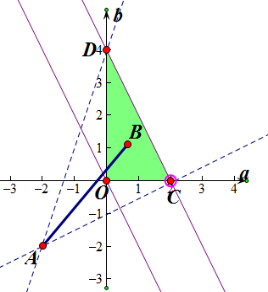
∴k就是可行域内的动点B(a,b)与定点A(-2,-2)连线的斜率
∵kAD=
=3,kAC=
=
,
∴k的范围为(
,3),
即求
的取值范围为(
,3)
 解:令x=y=2,则f(2×2)=f(2)+f(2),
解:令x=y=2,则f(2×2)=f(2)+f(2),∴f(4)=2f(2)=2×1=2.
∵f(2a+b)<2=f(4),f(x)是定义在(0,+∞)上的增函数
∴2a+b<4
∵2a+b>0,由线性规化可得关于(a,b)可行域,
∵设k=
| b+2 |
| a+2 |
| b-(-2) |
| a-(-2) |
∴k就是可行域内的动点B(a,b)与定点A(-2,-2)连线的斜率
∵kAD=
| 4+2 |
| 2 |
| 2 |
| 2+2 |
| 1 |
| 2 |
∴k的范围为(
| 1 |
| 2 |
即求
| b+2 |
| a+2 |
| 1 |
| 2 |
点评:本题考查了抽象函数的求值及利用线性规划求取值范围,关键
转化为斜率的问题,属于中档题.
| b+2 |
| a+2 |

练习册系列答案
相关题目