题目内容
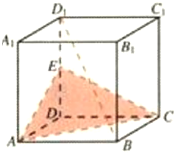 如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,
如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,(1)求证:BD1∥平面ACE
(2)求三棱锥E-ACD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结AC,BD,交于点O,连结OE,由已知得OE∥BD1,由此能证明BD1∥平面ACE.
(2)由已知得DE⊥平面ACD,且DE=1,S△ACD=
×2×2=2,由此能求出三棱锥E-ACD的体积.
(2)由已知得DE⊥平面ACD,且DE=1,S△ACD=
| 1 |
| 2 |
解答:
(1)证明:连结AC,BD,交于点O,连结OE,
∵ABCD是正方体,∴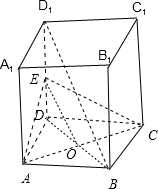 O是BD中点,
O是BD中点,
∵E是DD1的中点,∴OE∥BD1,
∵BD1不包含于平面ACE,OE?平面ACE,
∴BD1∥平面ACE.
(2)解:∵正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,
∴DE⊥平面ACD,且DE=1,S△ACD=
×2×2=2,
∴三棱锥E-ACD的体积:
V=
S△ACD•DE=
×2×1=
.
∵ABCD是正方体,∴
 O是BD中点,
O是BD中点,∵E是DD1的中点,∴OE∥BD1,
∵BD1不包含于平面ACE,OE?平面ACE,
∴BD1∥平面ACE.
(2)解:∵正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,
∴DE⊥平面ACD,且DE=1,S△ACD=
| 1 |
| 2 |
∴三棱锥E-ACD的体积:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查直线与平面平行的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}满足a1=0,an+1=
,则a31是( )
an-
| ||
|
| A、0 | ||||
B、-
| ||||
C、
| ||||
D、
|
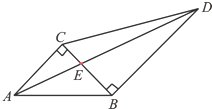 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.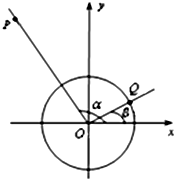 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为