题目内容
求过点P（1，6），且分别满足下列条件的直线方程：
（1）与直线x-3y+4=0垂直；
（2）与圆（x+2）2+（y-2）2=25相切．
（1）与直线x-3y+4=0垂直；
（2）与圆（x+2）2+（y-2）2=25相切．
考点：圆的切线方程,直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：（1）可设垂线：3x+y+m=0，把点P（1，6）代入解得即可．
（2）设出所求直线的斜率，求出圆的圆心与半径，列出方程求出直线的斜率，即可．
（2）设出所求直线的斜率，求出圆的圆心与半径，列出方程求出直线的斜率，即可．
解答：
解：（1）由两条直线垂直，可设垂线：3x+y+m=0，
∵垂线过点P（1，6），∴3×1+6+m=0
解得：m=-9，∴所求垂线的方程为：3x+y-9=0．
（2）的切线斜率存在时，设所求直线的斜率为k，由题意可得y-6=k（x-1），即kx-y+6-k=0．
圆（x+2）2+（y-2）2=25的圆心 （-2，2），半径为：5．
由题意可得：
=5，解得k=-
．
所求直线方程为：3x+4y-27=0．
当直线的斜率不存在时，切线方程为x=1，满足题意．
所求直线方程为：3x+4y-27=0或x=1．
∵垂线过点P（1，6），∴3×1+6+m=0
解得：m=-9，∴所求垂线的方程为：3x+y-9=0．
（2）的切线斜率存在时，设所求直线的斜率为k，由题意可得y-6=k（x-1），即kx-y+6-k=0．
圆（x+2）2+（y-2）2=25的圆心 （-2，2），半径为：5．
由题意可得：
| |-2k-2+6-k| | ||
|
| 3 |
| 4 |
所求直线方程为：3x+4y-27=0．
当直线的斜率不存在时，切线方程为x=1，满足题意．
所求直线方程为：3x+4y-27=0或x=1．
点评：本题考查直线方程的求法，直线与圆的位置关系的应用，考查计算能力．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
“直线l经过平面α内一点P，但l在α外”用符号表示正确的是（ ）
| A、P?l，P?α，l?α |
| B、P∈l，P∈α，l?α |
| C、P∈l，P?α，l∉α |
| D、P∈l，P∈α，l∉α |
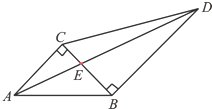如图，两块直角三角板拼在一起，已知∠ABC=45°，∠BCD=60°．