题目内容
已知
=（0，1，1），
=（-1，3，0），
（1）若k
-
与
+
互相垂直，求实数k的值；
（2）若
=（x，1，1），且|
-
|=
，求实数x的值．
| a |
| b |
（1）若k
| a |
| b |
| a |
| b |
（2）若
| c |
| b |
| c |
| 5 |
考点：平面向量数量积的坐标表示、模、夹角
专题：空间向量及应用
分析：（1）根据两非零向量垂直的充要条件，即可建立关于k的方程，解方程即得k的值；
（2）先求向量
-
的坐标，根据坐标表示出向量
-
的长度，即可建立关于x的方程，解方程即得x的值．
（2）先求向量
| b |
| c |
| b |
| c |
解答：
解：（1）k
-
=(1，k-3，k)，
+
=(-1，4，1)，由k
-
与
+
互相垂直可知：(k
-
)•(
+
)=-1+4(k-3)+k=0，得：k=
；
（2）
-
=(-1-x，2，-1)，由条件可知：
=
，解得：x=-1；
即实数x的值为：-1．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 13 |
| 5 |
（2）
| b |
| c |
| (-1-x)2+5 |
| 5 |
即实数x的值为：-1．
点评：考查两非零向量互相垂直的充要条件，向量数量积的坐标运算，用坐标表示向量的长度．
练习册系列答案
阅读快车系列答案
相关题目
已知向量
=（sinα，cosα），
=（cosβ，sinβ），且
∥
，则α+β等于（ ）
| a |
| b |
| a |
| b |
| A、0° | B、90° |
| C、135° | D、180° |
已知数列{an}满足a1=0，an+1=
，则a31是（ ）
an-
| ||
|
| A、0 | ||||
B、-
| ||||
C、
| ||||
D、
|
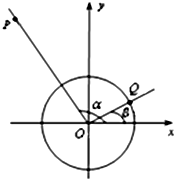如图所示，已知α的终边所在直线上的一点P的坐标为（-3，4），β的终边在第一象限且与单位圆的交点Q的纵坐标为