题目内容
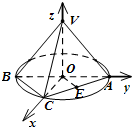
 如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.
如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.(Ⅰ)求证:OE∥平面VBC;
(Ⅱ)求证:VO⊥面ABC;
(Ⅲ)已知θ是平面VBC与平面VOE所形成的二面角的平面角,且0°<θ<90°,若OA=OV=1,求cosθ的值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)要证OE∥平面VBC,只需证OE平行于平面VBC内的一条直线即可;
(Ⅱ)要证VO⊥平面ABC,只需证VO垂直于平面ABC内的两条相交直线即可;
(Ⅲ)建立空间直角坐标系,求出平面VBC、平面VOE的法向量,利用向量的夹角公式,即可求cosθ的值.
(Ⅱ)要证VO⊥平面ABC,只需证VO垂直于平面ABC内的两条相交直线即可;
(Ⅲ)建立空间直角坐标系,求出平面VBC、平面VOE的法向量,利用向量的夹角公式,即可求cosθ的值.
解答:
 (Ⅰ)证明:∵O,E分别是AB和AC的中点,∴OE∥BC.--------------(2分)
(Ⅰ)证明:∵O,E分别是AB和AC的中点,∴OE∥BC.--------------(2分)
又∵OE?面VBC,BC?面VBC.----------------------------(3分)
∴OE∥面VBC.-----------------------------------------(4分)
(Ⅱ)证明:∵VA=VB,∵△ABC为等腰三角形,
又∵O为AB中点,∴VO⊥AB;--------------------------------(5分)
在△VOA和△VOC中,OA=OC,VO=VO,VA=VC,△VOA≌△VOC;--------(6分)
∴∠V0A=∠VOC=90°.∴VO⊥OC;--------------------------------------(7分)
∵AB∩OC=O,AB?平面ABC,OC?平面ABC,---------------------(8分)
∴VO⊥平面ABC.---------------------------------------------------(9分)
(Ⅲ)解:在圆O内,OA=OC,∠CAO=45°,所以CO⊥AO.
由(Ⅱ)VO⊥平面ABC,如图,建立空间直角坐标系.-------------------------(10分)
∵OA=OB=OC=OV=1,
∴C(1,0,0),A(0,1,0),B(0,-1,0),V(0,0,1),E(
,
,0).(11分)
∴
=(-1,-1,0),
=(-1,0,1)
设
=(x,y,z)为平面VBC的法向量,则
,
∴
,令x=1,解得
=(1,-1,1).----------------------(12分)
同理,求得平面VOE的法向量为
=(1,-1,0).--------------------(13分)
∴cos<
,
>=
=
=
,
∴cosθ=
.----------------------------------------------(14分)
 (Ⅰ)证明:∵O,E分别是AB和AC的中点,∴OE∥BC.--------------(2分)
(Ⅰ)证明:∵O,E分别是AB和AC的中点,∴OE∥BC.--------------(2分)又∵OE?面VBC,BC?面VBC.----------------------------(3分)
∴OE∥面VBC.-----------------------------------------(4分)
(Ⅱ)证明:∵VA=VB,∵△ABC为等腰三角形,
又∵O为AB中点,∴VO⊥AB;--------------------------------(5分)
在△VOA和△VOC中,OA=OC,VO=VO,VA=VC,△VOA≌△VOC;--------(6分)
∴∠V0A=∠VOC=90°.∴VO⊥OC;--------------------------------------(7分)
∵AB∩OC=O,AB?平面ABC,OC?平面ABC,---------------------(8分)
∴VO⊥平面ABC.---------------------------------------------------(9分)
(Ⅲ)解:在圆O内,OA=OC,∠CAO=45°,所以CO⊥AO.
由(Ⅱ)VO⊥平面ABC,如图,建立空间直角坐标系.-------------------------(10分)
∵OA=OB=OC=OV=1,
∴C(1,0,0),A(0,1,0),B(0,-1,0),V(0,0,1),E(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| CB |
| CV |
设
| m |
|
∴
|
| m |
同理,求得平面VOE的法向量为
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 1+1 | ||||
|
| ||
| 3 |
∴cosθ=
| ||
| 3 |
点评:本题考查线面平行,线面垂直的判定定理,考查面面角,正确运用线面平行,线面垂直的判定定理,求出平面的法向量是关键.

练习册系列答案
相关题目
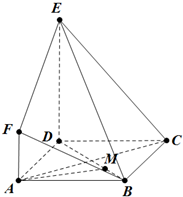 如图,ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3.
如图,ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3.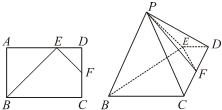 如图,在矩形ABCD中,点E为边AD上的点,点F为边CD的中点,AB=AE=
如图,在矩形ABCD中,点E为边AD上的点,点F为边CD的中点,AB=AE=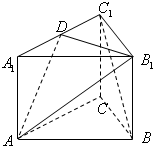 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
 已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.
已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.